주어진 시작 조건에서, n차원의 선형 미분 방정식을 풉니다. 솔루션은 기본 행렬의 고유값과 고유벡터의 결정에 기초합니다. 솔루션은 기호형태로 주어집니다.


icon

입력/출력

  • c2ddbl.png A (계수의 행렬) —

    A는 선형 시스템을 나타내는 n x n 행렬입니다.

  • c1ddbl.png X0 (시작값) —

    X0는 시작 조건, x[10], …, x[n0]를 나타내는 n 벡터입니다.

    X0와 X의 구성요소는 일대일 관계입니다.

  • istr.png 수식 —

    수식은 LabVIEW의 표준 수식 표기로 선형 시스템의 솔루션을 가지는 문자열입니다. 솔루션 벡터 원소는 캐리지 리턴으로 분리되어 있습니다.

  • ii32.png 에러 —

    에러는 VI로부터 모든 에러 또는 경고를 반환합니다. 에러는 잘못된 입력 X, X0, F(X,t)의 사용으로 생성됩니다. 에러를 [에러 코드를 에러 클러스터로] VI에 연결하여 에러 코드 또는 경고를 에러 클러스터로 변환할 수 있습니다.

    • 노트 이 VI는 반복되는 고유값, 켤레 복소수 고유값 등을 가질 수 있는 실수 행렬 A의 대부분의 경우에 올바르게 작동합니다. 예외는 특이한 고유벡터 행렬, 즉 고유벡터가 전체 공간에 미치지 않는 행렬의 경우입니다. 고유 벡터 행렬이 특이하면 -23016의 오차가 주어집니다.

    선형 미분 방정식은 다음 시스템으로 나타냅니다.

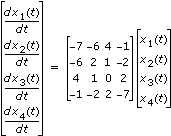
    이 때

    x1(0) = 1 x2(0) = 2 x3(0) = 3 x4(0) = 4

    솔루션은 다음과 같습니다.

    + 1.62*E(-12.46*T) - 1.28*E(-6.30*T) + 0.63*E(1.34*T) + 0.04*E(5.42*T) + 0.84*E(-12.46*T) - 0.29*E(-6.30*T) + 1.51*E(1.34*T) - 0.06*E(5.42*T) -0.73*E(-12.46*T) + 0.01*E(-6.30*T) + 3.69*E(1.34*T) + 0.02*E(5.42*T) + 0.87*E(-12.46*T) + 2.67*E(-6.30*T) + 0.45*E(1.34*T) + 0.01*E(5.42*T)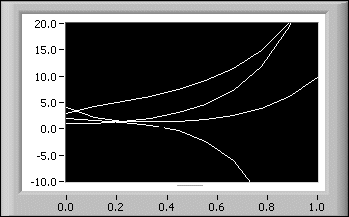

    다음 파라미터의 리스트는 위의 방정식을 프런트패널에 입력하는 방식을 나타냅니다:

    • A: [-7, -6, 4, 1; -6, 2, 1, -2; 4, 1, 0, 2; -1, -2, 2, -7]
    • X0: [1, 2, 3, 4]