주어진 시작 조건에서, 상수 계수를 가지는 n차원의 선형 동차 미분 방정식을 풉니다.


icon

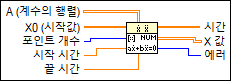
입력/출력

  • c2ddbl.png A (계수의 행렬) —

    A는 선형 시스템을 나타내는 n x n 행렬입니다.

  • c1ddbl.png X0 (시작값) —

    X0는 시작 조건, x[10], …, x[n0]를 나타내는 n 벡터입니다.

    X0와 X의 구성요소는 일대일 관계입니다.

  • cu32.png 포인트 개수 —

    포인트 개수는 시작 시간과 끝 시간 사이에서 등거리 시간 포인트의 개수입니다. 기본값은 10입니다.

  • cdbl.png 시작 시간 —

    시작 시간은 ODE의 시작 포인트입니다. 기본값은 0입니다.

  • cdbl.png 끝 시간 —

    끝 시간은 실행 중인 시간 간격의 끝 포인트입니다. 기본값은 1.0입니다.

  • i1ddbl.png 시간 —

    시간은 시간 단계를 나타내는 배열입니다. 이 방법은 시작 시간과 끝 시간 사이의 등거리 시간 간격을 만듭니다.

  • i2ddbl.png X 값 —

    X 값은 등거리 시간 포인트에서의 솔루션 X의 행렬입니다.

  • ii32.png 에러 —

    에러는 VI로부터 모든 에러 또는 경고를 반환합니다. 에러는 잘못된 입력 X, X0, F(X,t)의 사용으로 생성됩니다. 에러를 [에러 코드를 에러 클러스터로] VI에 연결하여 에러 코드 또는 경고를 에러 클러스터로 변환할 수 있습니다.

    • 이 VI의 솔루션은 기본 행렬 A의 고유값과 고유벡터의 결정에 기초합니다. 솔루션은 숫자 형태로 주어집니다.

    노트 이 VI는 반복되는 고유값, 켤레 복소수 고유값 등을 가질 수 있는 실수 행렬 A의 대부분의 경우에 올바르게 작동합니다. 예외는 특이 고유벡터 행렬, 즉 고유벡터가 전체 공간에 미치지 않는 행렬의 경우입니다. 고유 벡터 행렬이 특이하면 -23016의 오차가 주어집니다.

    선형 시스템은 다음과 같이 표시됩니다.

    X(0) = X0

    시작 시간 = 0인 경우입니다.

    여기서

    X(t) = (x0(t), …, xn(t))

    그리고 A는 n x n 실수 행렬을 나타냅니다. 선형 시스템은 A의 고유값과 고유벡터를 결정하여 풀 수 있습니다. S을 전체 n차원 공간에 미치는 모든 고유벡터의 세트로 가정합니다. 변환 Y(t) = SX(t)의 결과는 다음과 같습니다.

    Y(0) = SX0

    행렬 SAS–1은 대각형이므로 솔루션은 명백합니다. 솔루션 X(t)는 역 변환으로 결정될 수 있습니다.

    X(t) = S–1Y(t)
    노트 필수적인 작업은 행렬 A의 고유벡터와 고유값의 계산이므로 Tick 출력은 실행되지 않습니다. 이 작업은 상대적으로 작은 A의 차원에 대해서는 무시할 수 있습니다.

    다음 그림은 다음의 시스템으로 표현되는 선형 미분 방정식의 솔루션의 네 구성요소를 나타냅니다.

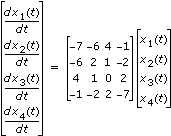
    이 때

    x1(0) = 1 x2(0) = 2 x3(0) = 3 x4(0) = 4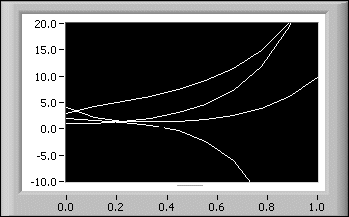

    다음 파라미터의 리스트는 위의 방정식을 프런트패널에 입력하는 방식을 나타냅니다:

    • A: [-7, -6, 4, 1; -6, 2, 1, -2; 4, 1, 0, 2; -1, -2, 2, -7]
    • X0: [1, 2, 3, 4]
    • 시작 시간: 0.00
    • 끝 시간: 1.00