오일러법을 사용하여 초기 조건을 가진 상미분 방정식을 풉니다.


icon

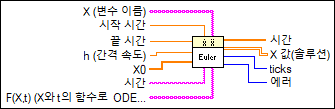
입력/출력

  • c1dstr.png X (변수 이름) —

    X는 변수 문자열의 배열입니다.

  • cdbl.png 시작 시간 —

    시작 시간은 ODE의 시작 포인트입니다. 기본값은 0입니다.

  • cdbl.png 끝 시간 —

    끝 시간은 실행 중인 시간 간격의 끝 포인트입니다. 기본값은 1.0입니다.

  • cdbl.png h (간격 속도) —

    h는 고정된 단계 속도입니다. 기본값은 0.1입니다.

  • c1ddbl.png X0 —

    X0는 시작 조건 x[10], …, x[n0]의 벡터입니다.

    X0와 X의 구성요소는 일대일 관계입니다.

  • cstr.png 시간 —

    시간은 시간 변수를 표시하는 문자열입니다. 기본 변수는 t입니다.

  • c1dstr.png F(X,t) (X와 t의 함수로 ODE의 우변) —

    F(X,t)는 미분 방정식의 우변을 나타내는 문자열의 1D 배열입니다. 수식은 개수의 제한 없이 유효한 변수를 포함할 수 있습니다.

  • i1ddbl.png 시간 —

    시간은 시간 단계를 나타내는 배열입니다. 오일러 방법은 시작 시간과 끝 시간 사이의 등거리 시간 간격을 만듭니다.

  • i2ddbl.png X 값(솔루션) —

    X 값은 솔루션 벡터 x[10], …, x[n]의 2D 배열입니다.

    최상위 인덱스는 시간 배열에 지정된 시간 간격을 따라서 실행되고 최하위 인덱스는 x[10], …, x[n]의 원소를 따라서 실행됩니다.

  • iu32.png ticks —

    Tick은 밀리초 단위에서 함수의 전체 계산에 대한 시간입니다.

  • ii32.png 에러 —

    에러는 VI로부터 모든 에러 또는 경고를 반환합니다. 에러는 잘못된 입력 X, X0, F(X,t)의 사용으로 생성됩니다. 에러를 [에러 코드를 에러 클러스터로] VI에 연결하여 에러 코드 또는 경고를 에러 클러스터로 변환할 수 있습니다.

    • 상미분 방정식(ODE)의 일반 형은 다음과 같습니다.

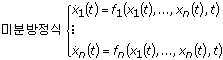
    이 때

    함수 f1, …, fn, 숫자, 시작 포인트 t = t0는 주어집니다. F = (f1, …, fn); X(t) = (x1(t), …, xn(t)); 그리고 X0 = (x10, …, xn0)의 형식을 사용하여

    다음을 얻습니다.

    위의 방정식을 만족시키는 함수 X를 결정해야 합니다.

    오일러법은 가장 기본적인 방법으로 상미분 방정식을 푸는데 유용합니다. 일반적인 경우 상대적으로 작고, 새로운 값인t0와 고정된 단계 속도 h로 시작하여

    X(t0 + h) = X(t0) +hF(X(t0), t) X(t0 +2h) = X(t0 + h) +hF(X(t0 + h),t0 + h) ⋮

    가 계산됩니다. 이 프로세스는 시간 시작 +nh ≥ 시간 종료인 경우 중지되며, 여기서 시간 종료는 조사 중인 시간 간격의 올바른 종료점입니다.

    다음 그림은 다음 상미분 방정식의 솔루션을 나타냅니다.

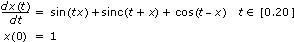
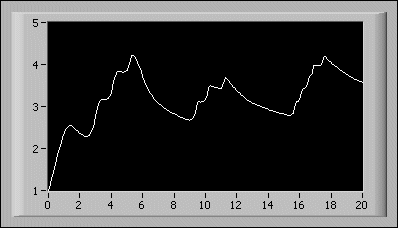
    위의 방정식과 초기 조건을 다음과 같이 프런트패널에 입력합니다:

    • 시작 시간: 0.00
    • 끝 시간: 20.00
    • X0: 1.00
    • F(X,t): sin(t*x) + sinc(t + x) + cos(t - x)
    • X: x