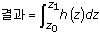수치 적분
- 업데이트 날짜:2025-07-30
- 3분 (읽기 시간)
네가지 일반적인 수치 적분 방법 중 하나를 사용하여 입력 배열의 수치 적분을 수행합니다. 데이터를 입력 배열 입력에 연결하여 사용할 다형성 인스턴스를 결정하거나 인스턴스를 수동으로 선택합니다.

이 VI에 연결하는 x 값은 균등한 간격이어야만 합니다. 그렇지 않으면 결과가 올바르게 나오지 않습니다. 값이 균등한 간격이 아닌 경우, [불균등한 수치 적분] VI를 사용하여 적분을 계산할 수 있습니다.
1D 수치 적분
| 포인트 개수 | 수행된 부분 계산 |
|---|---|
| 224 | 55 Bode, 1 Simpsons' 3/8 |
| 225 | 56 Bode |
| 226 | 56 Bode, Trapezoidal |
| 227 | 56 Bode, 1 Simpsons' |
| 228 | 57 Bode, 1 Simpsons' 3/8 |
224 포인트가 주어지고 Bode 방법이 선택된 경우, VI는 55 Bode 방법 부분 계산과 하나의 Simpsons' 3/8 방법 계산을 수행하여 결과를 도출합니다.
각 방법은 샘플링 간격(dt)을 따르며 몇몇 인접 포인트에 의존하는 부분 계산을 수행하기 위해서 기본 수식의 연속적인 어플리케이션을 사용하여 적분을 계산합니다. 각 부분 계산에 사용되는 포인트의 개수는 방법의 차수를 나타냅니다. 결과는 이런 연속적인 부분 계산의 합계입니다.
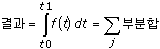
이 때 j는 포인트 개수와 적분 방법에 의존하는 범위입니다.
다음은 각 방법의 부분 합계를 계산하기 위한 기본 수식을 오름차순으로 나타낸 것입니다.
- Trapezoidal: 1/2(x[i] + x[i + 1])*dt
- Simpsons': (x[2i] + 4x[2i + 1] + x[2i + 2])*dt/3, k = 2
- Simpsons' 3/8: (3x[3i] + 9x[3i + 1] + 9x[3i + 2] + 3x[3i + 3]) * dt/8, k = 3
-
Bode: (14x[4i] +64x[4i + 1] +24x[4i + 2] +64x[4i + 3] +14x[4i + 4]) * dt/45, k = 4
i = 0, 1, 2, 3, 4, ...에 대해 [(N-1 )/k]의 적분 부분
이 때 N은 데이터 포인트 개수, k는 방법에 따른 정수, x는 입력 배열입니다.
2D 수치 적분
2D 수치 적분 수행에서
 ,
,이 VI는 계산을 위해 우선 1D 수치 적분을 x에 적용하고
 .
.다음으로 이 VI는 결과를 얻기 위해 1D 수치 적분을 y에 적용합니다
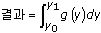
3D 수치 적분
3D 수치 적분 수행에서
 ,
,이 VI는 다음에 보이는 방정식과 같이 순차적으로 x, y 및 z에 대해 1D 수치 적분을 적용합니다.