스플라인 보간의 2차 도함수
- 업데이트 날짜:2025-07-30
- 4분 (읽기 시간)
길이 n인 보간의 2차 도함수 배열을 반환합니다. 이 보간은 표로 된 포인트 x[i]에서 스플라인 보간 함수 g(x)의 2차 도함수를 포함하며, 여기서 i = 0, 1, …, n–1입니다.
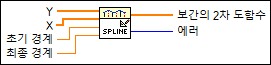
입력/출력
 Y
—
Y
—
Y는 종속적인 값의 배열입니다. X 원소의 개수가 Y 원소의 개수와 다른 경우, VI는 출력 보간의 2차 도함수를 빈 배열로 설정하고 에러를 반환합니다.  X
—
X
—
X는 독립적인 값의 배열입니다. X 원소의 개수가 Y 원소의 개수와 다른 경우, VI는 출력 보간의 2차 도함수를 빈 배열로 설정하고 에러를 반환합니다.  초기 경계
—
초기 경계
—
초기 경계는 x[0]에서 보간 함수 g(x)의 1차 도함수인 g'(x[0])입니다. 기본은 1.00E+30 이며, 이 값은 이 VI가 자연 스플라인에 대해서 초기 경계 조건을 설정하도록 합니다. g(x)의 정의에 대해서는 스플라인 보간의 2차 도함수를 참조하십시오.  최종 경계
—
최종 경계
—
최종 경계는 x[n – 1]에서 보간 함수 g(x)의 1차 도함수인 g'(x[n – 1])입니다. 기본은 1.00E+30 이며, 이 값은 이 VI가 자연 스플라인에 대해서 최종 경계 조건을 설정하도록 합니다.  보간의 2차 도함수
—
보간의 2차 도함수
—
보간의 2차 도함수는 x[i], i = 0, 1, …, n – 1 포인트에서 보간 함수 g(x)의 2차 도함수입니다. 보간을 스플라인 보간 VI의 입력으로 사용하여 x0 ≤ x < xn- 1의임의의 값으로 y를 보간할 수 있습니다.  에러
—
에러
—
에러는 VI로부터 모든 에러 또는 경고를 반환합니다. 에러를 [에러 코드를 에러 클러스터로] VI에 연결하여 에러 코드 또는 경고를 에러 클러스터로 변환할 수 있습니다. |
입력 배열 X와 Y는 길이가 n이며 표로 된 함수를 포함하고, x0 < x1 < … < xn - 1일 때 다음 방정식으로 나타냅니다:
f(xi) = yi보간 함수 g(x)는 다음 식의 구간별 함수합니다:
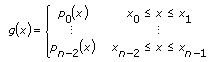
함수 pi(x)는 3차 다항식이며 반드시 다음 조건을 충족해야 합니다:
- g(xi) = yi = pi(xi)
- g(xi) = yi = pi – 1(xi)
- 각 내부 xi에서 i = 1, …, n – 2일 때 1차와 2차 도함수는 연속입니다:
- g'(xi) = p'i(xi) = p'i - 1(xi)
- g"(xi) = p"i(xi) = p"i – 1(xi)
세번째 조건에서 다음 방정식을 도출할 수 있습니다:
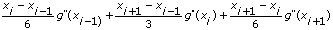 =
= 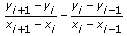
여기서 i = 1, …, n – 2. 이 식에 따르면, n개의 알려지지 않은 g"(xi)에 n – 2 선형 방정식이 있습니다.
이 [스플라인 보간의 2차 도함수] VI는 다음 방정식에서 x0 및 xn – 1에서의 도함수를 위한 두 식을 계산합니다:
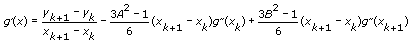
다음의 식을 고려하십시오:


초기 경계는 다음 식이며
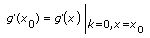
최종 경계는 다음 식입니다
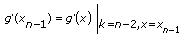 .
.이 식에서 초기 경계와 최종 경계는 각각 x0과 xn – 1 포인트에서 g(x) 의 1차 도함수입니다. 초기 경계와 최종 경계가 1030보다 크거나 같은 경우, 이 VI는 해당 경계의 2차 도함수 없이, 기본적인 스플라인의 대응하는 경계 조건을 설정합니다.
이 VI는 n 방정식에서 g"(xi)를 풀며, 여기서 i = 0, 1, …, n – 1입니다. g"(xi)는 보간 출력입니다.
예제
LabVIEW 포함되는 다음 예제 파일을 참조하십시오.
- labview\examples\Mathematics\Interpolation\Interpolation Solver.vi