분할표

입력/출력

우연도표 VI는 χ² 동질성 검정과 χ² 독립성 검정으로 가설을 테스트합니다. 가설을 검정하기 전에 각 검정에서의 확률 최소값을 결정합니다. 결정한 확률 최소값은 가설을 받아들이거나 거부하는 기준값입니다. 일반적으로, 확률에 대해 작은 값을 선택합니다. 0.05가 일반적인 선택값입니다. VI가 반환한 확률의 실제 값이 결정한 값보다 작은 경우, 가설의 거부를 고려합니다.

Χ² 동질성 테스트에서는 하나의 분류 체계에서 각 범주에서 일정 크기의 무작위 표본을 추출합니다. 각 샘플에 대해, VI는 두번째 방법에 따라 실험 객체를 분류하고 그것을 기록합니다. VI는 가설을 검정하여 각 샘플을 취한 모집단이 두번째 분류 방법에 관해서 동일하게 분포되었는지를 결정합니다.

Χ² 독립성 테스트에서는 전체 모집단에서 단 하나의 샘플만 사용합니다. VI는 그 후 각 객체를 분류하고 두 분류 방법으로 기록합니다. VI는 분류 방법이 독립적이라는 가설을 검정합니다.

수식

y_{p, q}는 분할표의 (pq)번째 셀의 어커런스 개수를 나타낸다고 가정합니다.

p = 0, 1, …, (s - 1) 및 q = 0, 1, …, (k - 1),

이 때 s는 분할표의 행의 개수, k는 분할표의 열의 개수입니다.

다음과 같은 식에서

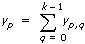
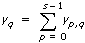
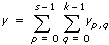
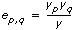
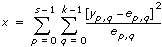
VI는 x를 사용하여 확률을 계산합니다.

p =확률{X ≥ x}

여기서 X는 χ² 분포의 무작위 변수입니다. 가설이 참이면 x는 (s - 1) 및(k - 1)의 자유도를 가진 χ² 분포에서 나옵니다.