3D ANOVA
- 업데이트 날짜:2025-07-30
- 9분 (읽기 시간)
세 인자의 여러 레벨에서 실시되는 실험적인 측정값의 배열을 취하고 삼원 분산분석을 수행합니다.

입력/출력
 레벨
—
레벨
—
레벨은 A, B, C 인자의 레벨 개수와 A, B, C 인자(고정되거나 임의의 값임)의 효과에 대응하는 세 숫자값의 클러스터입니다.
 X
—
X
—
X는 모든 측정 데이터를 포함합니다.  인덱스 A
—
인덱스 A
—
인덱스 A는 대응되는 측정이 속하는 인자 A의 레벨을 포함합니다.  인덱스 B
—
인덱스 B
—
인덱스 B는 대응되는 측정이 속하는 인자 B의 레벨을 포함합니다.  인덱스 C
—
인덱스 C
—
인덱스 C는 대응하는 측정이 속하는 인자 C의 레벨을 포함합니다.  셀당 측정 개수
—
셀당 측정 개수
—
셀당 측정 개수는 각 셀의 측정 개수입니다. 이것은 모든 셀에 대해서 동일합니다.  정보
—
정보
—
정보는 첫번째 열이 각 인자들(A, B, C), 각 상호작용들(AB, AC, BC, ABC), 잔차 에러에 연계된 제곱합에 대응하는 8 x 4로 구성된 행렬입니다. 두번째 열은 각각 자유도에 대응합니다. 세번째 열은 각각 제곱 평균에 대응합니다. 네번째 열은 각각 F 값에 대응합니다.   유의성
—
유의성
—
유의성은 유의 수준에 대응하는 7개 숫자값의 클러스터입니다.
 에러
—
에러
—
에러는 VI로부터 모든 에러 또는 경고를 반환합니다. 에러를 [에러 코드를 에러 클러스터로] VI에 연결하여 에러 코드 또는 경고를 에러 클러스터로 변환할 수 있습니다. |
모든 ANOVA에서, 인자 또는 인자 사이의 상호작용이 실험 결과에 상당한 영향을 미친다는 증거를 찾습니다. 각 모델에서 다른 점은 이를 위해 사용하는 방법입니다.
3D ANOVA 임의 및 고정 효과
결론을 도출하려는 레벨의 모집단 수가 많아 모든 레벨에서 샘플링을 할 수 없는 경우, 인자는 임의 효과입니다. 이 경우 임의로 레벨을 선택하여 모든 레벨에 적용되는 일반적인 결과를 도출합니다. 결론을 도출하려는 모든 레벨에서 샘플을 추출할 수 있는 경우 인자는 고정 효과입니다.
3D ANOVA 통계 모델
xpqrs는 각각 A,B,C의 p번째, q번째, r번째 레벨의 s번째 측정이며, 이때 s = 0, 1, ..., L – 1입니다. 각 측정을 여덟개의 구성 요소의 합으로 나타냅니다. 그러므로 다음과 같습니다.
xpqrs = µ + αp + βq + γr + (αβ)pq + (αγ)pr + (βγ)qr + (αβγ)pqr + εpqrs여기에서
- μ 는 총 평균입니다.
- αp 는 요인 A의p번째 레벨의 평균 효과입니다.
- βq 는 요인 B의q번째 레벨의 평균 효과입니다.
- γr 는 요인 C의r번째 레벨의 평균 효과입니다.
- (αβ)pq 는 요인 A의p번째 수준과 요인 B의q번째 수준의 2요인 상호작용입니다.
- (αγ)pr 은 요인 A의p번째 수준과 요인 C의r번째 수준의 2요인 상호작용입니다.
- (βγ)qr 은 요인 B의q번째 수준과 요인 C의r번째 수준의 2요인 상호작용입니다.
- (αβγ)pqr 은 요인 A의p번째 수준, 요인 B의q번째 수준, 요인 C의r번째 수준의 3요인 상호 작용입니다.
- εpqrs 는 무작위 변동입니다.
3D ANOVA 가설
다음의 각 가설은 인자 또는 인자 사이의 상호작용이 실험 결과에 영향을 미치지 않는다는 것을 다른 방법으로 표현한 것입니다. 이 VI는 영향이 없다고 가정한 후 이 가정에 반하는 증거를 찾습니다. 다음은 일곱가지 가설입니다:
- (A) αp = 는 요인 A가 고정된 경우 모든 레벨 p에 대해 0이고, 요인 A가 무작위인 경우σA²= 0입니다.
- (B) βq = 는 모든 레벨 q에 대해 0이고, 요인 B가 고정된 경우σB²는무작위인 경우 0입니다.
- (C) γr = 요인 C가 고정된 경우 모든 레벨 r에 대해 0이고, 요인 B가 무작위인 경우σC²= 0입니다.
- (AB) 그 (αβ)pq = 는 요인 A와 B가 고정된 경우 모든 수준 p와 q에 대해 0이고, 요인 A 또는 B가 무작위인 경우σAB²= 0입니다.
- (AC) 그 (αγ)pr = 는 요인 A와 C가 고정된 경우 모든 레벨 p와 q에 대해 0이고, 요인 A 또는 C가 무작위인 경우σAC²= 0입니다.
- (BC) 그 (βγ)qr = 는 요인 B와 C가 고정된 경우 모든 레벨 p와 q에 대해 0이고, 요인 B 또는 C가 무작위인 경우σBC²= 0입니다.
- (ABC) 그 (αβγ)pqr = 요인 A, B, C가 고정된 경우 모든 수준 p, q, r에 대해 0이고, 요인 A, B, C 중 하나라도 무작위인 경우σABC²= 0입니다.
3D ANOVA 가정
[3D ANOVA] VI는 다음을 가정합니다:
- 각 p, q, r에대해 εpqrs 가 평균 0, 분산σe²로정규 분포한다고 가정합니다.
- 요인 A가 고정된 경우, A의 각 수준에서 측정값의 모집단이 평균 α로 정규 분포한다고 가정합니다p + µ 및 분산σA²로정규 분포되어 있고 각 수준의 모든 모집단의 분산이 동일하다고 가정합니다. 또한 αp 합이 0이라고 가정합니다. B와 C에 대해서도 마찬가지로 가정합니다.
- 인자 A가 무작위인 경우, 인자 A 자체의 레벨 효과인 αp는 평균 0, 분산σA²로정규 분포하는 확률 변수입니다. B와 C에 대해서도 마찬가지로 가정합니다.
- 상호 작용의 효과와 관련된 요인(예: A 및 B) 중 일부가 (αβ)인 경우pq 로 고정된 경우, A와 B의 각 수준에서 측정값의 모집단이 평균 µ + α로 정규 분포한다고 가정합니다p + βq + (αβ)pq 및 분산σAB². 고정된 p의경우, 평균(αβ)pq 는 모든 q를합산할 때 0이 됩니다. 마찬가지로, 고정된 q의경우 (αβ)pq 는 모든 p를합산할 때 0이 됩니다.
- 상호작용의 효과(αβ)와 관련된 요인(예: A 및 B) 중 하나라도 있는 경우pq 가 무작위인 경우, 그 효과가 평균 0, 분산σAB²로정규 분포된 확률 변수라고 가정합니다. A가 고정되어 있고 B가 무작위인 경우, 고정된 q에대해 평균(αβ)은 다음과 같다고 가정합니다pq 를모두 합산하면 0이 된다고 가정합니다. 마찬가지로, B가 고정되어 있고 A가 무작위인 경우, 고정된 p에 대해 평균(αβ)은 다음과 같다고 가정합니다pq 를모두 합산하면 0이 된다고 가정합니다.
- 확률 변수에 적용된 모든 효과는 상호 독립적이라고 가정합니다.
3D ANOVA 일반적인 방법
각 모델에서, VI는 전체 모집단 평균으로부터 데이터의 전체 변동을 측정한 전체 제곱합, tss를 여러 구성요소의 제곱합으로 분해합니다.
tss = ssa + ssb + ssc + ssab + ssac + ssbc + ssabc + sse합계 tss의 각 구성요소는 특정 인자 또는 인자 사이의 상호작용에 기인한 변동 측정입니다. 여기서 ssa는 인자 A로 인한 변동 측정이며, ssb는 인자 B로 인한 변동 측정, ssc는 인자 C로 인한 변동 측정, ssab는 인자 A와 B사이의 상호작용으로 인한 변동 측정이며, ssac, ssbc, ssabc도 마찬가지입니다. 또한, sse는 임의의 변동으로 인한 변동 측정입니다. VI는 각각을 고유의 자유도로 나누어 대응하는 평균 msa, msb, msc, msab, msac, msbc, msabc, mse를 얻습니다. 예를 들어, 인자 A가 실험 측정에 큰 영향을 미치는 경우, msa는 상대적으로 큽니다.
3D ANOVA 가설 검정하기
각 가정에 대해, VI는 관련된 유의성 확률을 계산하는데 사용되는 숫자 f를 계산합니다. 예를 들어, 모든 레벨 p에 대해 p = 0 라는 가설 (A) (고정된 A)에 대해, VI는 다음을 계산합니다.

그리고
sigA = Prob{Fa – 1, abc(L – 1) > fa}여기에서
Fa – 1, abc(L – 1)는 자유도가 a - 1과 abc(L - 1)인 F 분포입니다. 확률 유의성 A, 유의성 B, 유의성 C, 유의성 AB, ... , 유의성 ABC를 사용하여 언제 관련된 가설 (A), (B), (C), (AB), ... , (ABC)를 거부할지 결정할 수 있습니다.
귀무 가설을 거부하는 시점을 어떻게 알 수 있을까요? 각 가설에 대해서 유의수준을 설정합니다. 이 유의수준은 실수로 가설을 거부하게 될 확률입니다.(일반적으로 0.05를 선택) 선택된 유의수준을 관련된 유의성 확률 출력과 비교합니다. 유의성 확률이 선택된 유의수준보다 작은 경우, 귀무 가설을 거부해야 합니다. 예를 들어 A가 무작위 효과이고 유의 수준이 0.05이고 sigA = 0.03인 경우,σA²= 0이라는 가설을 거부하고 요인 A가 실험 관찰에 영향을 미친다는 결론을 내려야 합니다.
몇몇 모델의 경우 특정 가설에 적절한 검정이 없습니다. 이러한 경우, 해당 가정의 검정과 직접 관련된 출력 파라미터는 -1.0 입니다.
3D ANOVA 수식
xpqrs는 각각 A,B,C의 p번째, q번째, r번째 레벨의 s번째 측정이며, 이때 s = 0, 1, ..., L – 1입니다.
다음과 같은 식에서
a = |A 레벨|
b = |B 레벨|
c = |C 레벨|
그리고
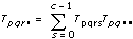
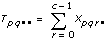
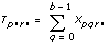
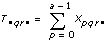

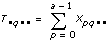
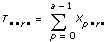
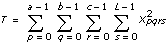
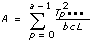
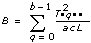
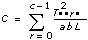
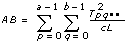




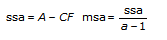
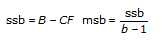
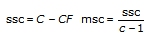
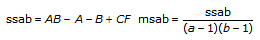


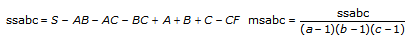
 유의성 A
—
유의성 A
—