1D ANOVA
- 업데이트 날짜:2025-07-30
- 5분 (읽기 시간)
하나의 인자에 대해 여러 레벨에서 취한 실험적인 측정 데이터의 배열 X를 레벨당 적어도 한번 측정해서 얻고 고정된 효과를 지닌 이 모델에서 1D ANOVA를 수행합니다.

입력/출력
 X
—
X
—
X는 모든 측정 데이터를 포함합니다.  인덱스
—
인덱스
—
인덱스에 대응하는 측정이 속해있는 레벨이 포함됩니다.  레벨 개수
—
레벨 개수
—
레벨 개수는 전체 레벨 개수입니다.  f
—
f
—
f는 f = msa/mse 인 비율입니다.  ssa
—
ssa
—
ssa는 전환율에 기인한 변동의 측정입니다.  sse
—
sse
—
sse는 임의의 변동에 기인한 변동의 측정입니다.  mse
—
mse
—
mse는 sse에 연계된 제곱 평균값입니다. 이것은 sse를 해당 자유도로 나누어 계산됩니다.  msa
—
msa
—
msa는 ssa에 연계된 제곱 평균값입니다. 이것은 ssa를 해당 자유도로 나누어 계산됩니다.  tss
—
tss
—
tss는 전체 모집단 평균에서 데이터의 총 변동을 측정한 전체 제곱의 합입니다. 이것은 tss = ssa + sse 를 사용하여 계산됩니다.  에러
—
에러
—
에러는 VI로부터 모든 에러 또는 경고를 반환합니다. 에러를 [에러 코드를 에러 클러스터로] VI에 연결하여 에러 코드 또는 경고를 에러 클러스터로 변환할 수 있습니다.  유의성 A
—
유의성 A
—
유의성 A는 주어진 특정 f에서 F 분포로부터 샘플링할 때 f보다 큰 값을 얻게 될 확률입니다. |
일원 분산분석에서, VI는 인자의 레벨이 실험 결과에 영향을 미치는지 여부를 테스트합니다.
1D ANOVA 인자와 레벨
인자는 데이터를 분류하는 기준입니다. 예를 들어, 개인이 할 수 있는 윗몸 일으키기의 횟수를 세는 경우, 분류의 한 기준은 나이입니다. 나이를 다음 레벨로 분류할 수 있습니다.
| 레벨 0 | 6세부터 10세 |
| 레벨 1 | 11세부터 15세 |
| 레벨 2 | 16세부터 20세 |
이제, 할 수 있는 윗몸 일으키기의 횟수를 조사하기 위해 일련의 측정을 한다고 가정합니다. 다섯명의 무작위 샘플링을 취하는 경우, 다음과 같은 결과가 나왔습니다.
| 첫번째 대상 | 8세(레벨 0) | 윗몸 일으키기 10회 |
| 두번째 대상 | 12세(레벨 1) | 윗몸 일으키기 15회 |
| 세번째 대상 | 16세(레벨 2) | 윗몸 일으키기 20회 |
| 네번째 대상 | 20세(레벨 2) | 윗몸 일으키기 25회 |
| 다섯번째 대상 | 13세(레벨 1) | 윗몸 일으키기 17회 |
각 레벨 당 적어도 하나의 대상을 조사하였습니다. 분산분석을 수행하려면, 각 레벨 당 적어도 하나의 대상을 조사해야합니다.
분산분석을 실행하려면, 측정의 배열 X를 값 10, 15, 20, 25, 17로 지정합니다. 배열 인덱스는 각 측정이 적용되는 레벨(또는 항목)을 지정합니다. 이 경우, 인덱스는 값 0, 1, 2, 2, 1을 갖습니다. 마지막으로, 3개의 가능한 레벨이 있으므로, 레벨 개수 파라미터에 값 3을 전달합니다.
1D ANOVA 통계 모델
분산분석을 실행하여 각 실험 결과를 세 부분의 합계로 나타냅니다. xim를 i번째 레벨의 m번째 측정값으로 가정합니다. 이 경우 각 측정을 다음으로 나타냅니다.
xim = µ + αi + εim이 때 μ는 총 평균으로 불리는 표준 효과입니다.
αi는 요인의째 레벨의 효과로,째 레벨 α의 평균 간의 차이입니다i 와 전체 평균
µ(µi) = µ + αi및 εim 은 무작위 변동입니다.
1D ANOVA 가설
이 VI는 가설 αi i = 0, 1, ..., k - 1의 경우 α i = 0(여기서 k는 레벨수)이라는 가설을 테스트합니다. 즉, 귀무 가설이라고 불리는 이 가설은 어떤 레벨도 실험 결과에 영향을 미치지 않는다는 것을 가정하고, 그 반대의 증거를 찾습니다.
1D ANOVA 가정
각 레벨에서 측정값의 모집단이 평균 μi 와 분산σA²로정규 분포되어 있다고 가정하고 αi 의 합계가 0이라고 가정합니다. 마지막으로, 각 i와 m에대해 εim 이 평균 0, 분산σA²로정규 분포한다고 가정합니다.
1D ANOVA 일반적인 방법
이 VI는 총 제곱합인 tss를 계산합니다. tss는 전체 모집단 평균에서 데이터의 총 변동을 측정한 것입니다.
tss는 두 부분으로 구성됩니다: ssa는 인자에 영향을 받는 변동의 측정이고, sse는 임의의 변화에 영향을 받는 변동의 측정입니다. 즉,
tss = ssa + sse.VI는 ssa와 sse를 자체의 자유도로 나누어 ssa와 sse로부터 두 평균 제곱 값 msa와 mse를 계산합니다. mse에 대해 상대적으로 msa가 클수록, 인자는 실험 결과에 큰 영향을 미칩니다.
특히 귀무 가설이 참인 경우, 비율 f, f = msa/mse는 자유도가 k - 1과 n - k인 F 분포로 얻으며, 이를 이용하여 확률을 계산할 수 있습니다. 특정한 f가 주어졌을 때, 유의성 A는 이 분포에서 샘플링을 할 때 f보다 큰 값을 얻을 확률입니다.
1D ANOVA 가설 검정하기
실수로 귀무 가설을 거부할 확률을 정하여 귀무 가설을 언제 거부할 것인지를 결정합니다. 이것을 유의수준이라하며, 일반적으로 0.05를 선택합니다. 출력 유의성 A를 선택된 유의수준과 비교하여 귀무 가설을 받아들일지 여부를 결정합니다. 유의성 A가 선택된 유의수준보다 작은 경우, 귀무 가설을 거부합니다. 귀무 가설을 거부하는 경우, 적어도 한 레벨은 실험 결과에 어떤 영향을 미친다는 것을 인식해야 합니다.
1D ANOVA 수식
xim은 m = 0, 1, …, ni – 1이고 i = 0, 1, …, k – 1일 때, i번째 레벨에서 수행한 m번째 측정입니다. 이 때, ni는 i번째 레벨에서의 측정 개수이고 k = 레벨 개수입니다.
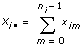
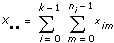
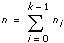
그리고
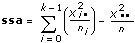
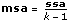
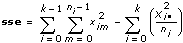

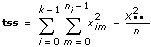

SigA = Prob{Fk - 1, n - k > f}
Fk – 1, n – k
는 자유도가 k - 1 과 n - k인 F 분포입니다.
예제
LabVIEW 포함되는 다음 예제 파일을 참조하십시오.
- labview\examples\Mathematics\Probability and Statistics\Unbalanced ANOVA on Rainfall Data.vi