입력 시퀀스 X와 Y의 합성곱을 계산합니다. 데이터를 X 또는 Y 입력에 연결하여 사용할 다형성 인스턴스를 결정하거나 인스턴스를 수동으로 선택합니다.


icon

입력/출력

  • c1ddbl.png X —

    X는 첫번째 입력 시퀀스입니다.

  • c1ddbl.png Y —

    Y는 두번째 입력 시퀀스입니다.

  • cenum.png 알고리즘 —

    알고리즘은 사용할 합성곱 방법을 지정합니다. 알고리즘이 direct일 때, 이 VI는 선형 합성곱의 다이렉트 방법을 사용하여 합성곱을 계산합니다. 알고리즘이 frequency domain일 때, 이 VI는 FFT 기반 기술을 사용하여 합성곱을 계산합니다.

    X와 Y가 작은 경우 일반적으로 direct 방식이 더 빠릅니다. X와 Y가 큰 경우 일반적으로 frequency domain 방식이 더 빠릅니다. 또한, 두 방법 사이에 약간의 숫자상 차이가 있을 수 있습니다.

    0
    direct
    1
    frequency domain
    (기본)
  • i1ddbl.png X * Y —

    X * Y는 X와 Y의 합성곱입니다.

  • ii32.png 에러 —

    에러는 VI로부터 모든 에러 또는 경고를 반환합니다. 에러를 [에러 코드를 에러 클러스터로] VI에 연결하여 에러 코드 또는 경고를 에러 클러스터로 변환할 수 있습니다.

    • 1D 합성곱

    x(t)와 y(t) 신호의 선형 합성곱을 다음과 같이 정의합니다:

    이 때 기호 *는 선형 합성곱을 나타냅니다.

    알고리즘이 다이렉트일 때, 이 VI는 다음 방정식을 사용해 선형 합성곱의 이산 실행을 수행하고 X*Y의 원소를 얻습니다.

    여기서 i = 0, 1, 2, … , M+N-2

    이때 h는 X * Y

    N은 X의요소 수입니다, M은 Y의요소 수입니다, 다음 관계와 같이 X와 Y의 범위를 벗어난 인덱싱된 요소는 0과 같습니다:

    xj = 0, j < 0 또는 j ≥ N

    및

    yj = 0, j < 0 또는 j ≥ M.

    알고리즘이 주파수 도메인일 때, 이 VI는 다음 단계를 순서대로 완료하여 선형 합성곱을 계산합니다:

    • 우선 이 VI는 X와 Y의 끝을 0으로 채워 다음 식과 같이 M + N의 길이가 -1이 되도록 만듭니다.
    • 두번째로 이 VI는 다음 방정식에 따라 X'와 Y'의 푸리에 변환을 계산합니다.
    X'(f) = FFT(x') Y'(f) = FFT(y')
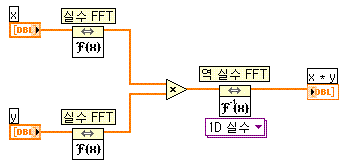
    • 세번째로 이 함수는 X'(f)에 Y'(f)를 곱하고 해당 곱의 역 푸리에 변환을 계산합니다. 결과는 다음 식과 같이 X와 Y의 선형 합성곱입니다.
    X * Y = IFFT(X'(f) · Y'(f))

    따라서 이 VI는 순환 합성곱이 아닌 선형 합성곱을 계산합니다. 그러나 x(t) * y(t)N ⇔ X(f)Y(f)는 푸리에 변환 쌍이며, 여기서 x(t) * y(t)N은 x(t)와 y(t)의 원형 컨볼루션이므로 원형 버전의 컨볼루션을 생성할 수 있습니다. 순환 합성곱을 계산하려면 다음 그림의 블록다이어그램과 비슷한 블록다이어그램을 사용합니다.

    예제

    LabVIEW 포함되는 다음 예제 파일을 참조하십시오.

    • labview\examples\Signal Processing\Signal Operation\Edge Detection with 2D Convolution.vi