入力シーケンスXの高速フーリエ変換 (FFT) を計算します。データをX入力に配線して使用する多態性インスタンスを決定するか、インスタンスを手動で選択します。


icon

1D FFT

1D信号では、FFT VIは高速フーリエ変換アルゴリズムで入力シーケンスの離散フーリエ変換 (DFT) を計算します。1D DFTは以下のように定義されます。

ここでn=0, 1, 2,…, N–1、

xは入力シーケンス、Nは xの要素数、Yは変換結果です。

周波数分解能、またはY 要素間の周波数間隔では、

fs がサンプリング周波数です。

以下の表は、さまざまなFFTサイズおよびシフト値のFFT {X}要素のパターンを示します。ここで、Y はFFT {X}、n は FFTサイズです。

n は偶数 (k = n/2)n は奇数 (k = (n-1)/2)
Shift 配列要素 相当する周波数 配列要素 相当する周波数

FALSE

(デフォルト)

 Y0 DC成分 Y0 DC成分

FALSE

(デフォルト)

 Y1 Δf Y1 Δf

FALSE

(デフォルト)

 Y2 2Δf Y2 2Δf

FALSE

(デフォルト)

 Y3 3Δf Y3 3Δf
⋮ ⋮ ⋮ ⋮ ⋮

FALSE

(デフォルト)

 Yk–2 (k-2）Δf Yk–2 (k-2）Δf

FALSE

(デフォルト)

 Yk–1 (k-1）Δf Yk–1 (k-1）Δf

FALSE

(デフォルト)

 Yk ナイキスト周波数 Yk kΔf

FALSE

(デフォルト)

 Yk+1 -(k-1)Δf Yk+1 -kΔf

FALSE

(デフォルト)

 Yk+2 -(k-2)Δf Yk+2 -(k-1)Δf
⋮ ⋮ ⋮ ⋮ ⋮

FALSE

(デフォルト)

 Yn–3 -3Δf Yn–3 -3Δf

FALSE

(デフォルト)

 Yn–2 -2Δf Yn–2 -2Δf

FALSE

(デフォルト)

 Yn–1 -Δf Yn–1 -Δf
n は偶数 (k = n/2)n は奇数 (k = (n-1)/2)
Shift 配列要素 相当する周波数 配列要素 相当する周波数
TRUE Y0 –(ナイキスト周波数) Y0 -kΔf
TRUE Y1 -(k-1)Δf Y1 -(k-1)Δf
TRUE Y2 -(k-2)Δf Y2 -(k-2)Δf
TRUE Y3 -(k-3)Δf Y3 -(k-3)Δf
⋮ ⋮ ⋮ ⋮ ⋮
TRUE Yk–2 -2Δf Yk–2 -2Δf
TRUE Yk–1 -Δf Yk–1 -Δf
TRUE Yk DC成分 Yk DC成分
TRUE Yk+1 Δf Yk+1 Δf
TRUE Yk+2 2Δf Yk+2 2Δf
⋮ ⋮ ⋮ ⋮ ⋮
TRUE Yn–3 (k-3）Δf Yn–3 (k-2）Δf
TRUE Yn–2 (k-2）Δf Yn–2 (k-1）Δf
TRUE Yn–1 (k-1）Δf Yn–1 kΔf

2D FFT

2D信号では、FFT VIは入力行列の離散フーリエ変換 (DFT) を計算します。このVIは入力行列の行で1D FFTを実行し、前の手順の出力列で1D FFT を実行します。M-x-N行列のDFTは以下のように定義されます。

u = 0, 1, ..., M-1, v = 0, 1, ..., N-1について

このとき、Xは入力行列、Yは変換結果です。

以下の図は、2D FFTの結果でのシフト?の効果を示します。

2D入力信号 シフトなしFFT シフト付きFFT

関連情報

FFTベースVIの出力単位

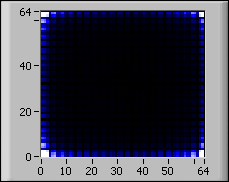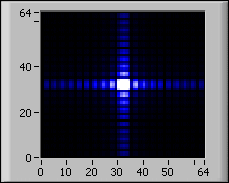サンプルプログラム

LabVIEWに含まれている以下のサンプルファイルを参照してください。

  • labview\examples\Signal Processing\Transforms\FFT and Power Spectrum Units.vi