コンボリューション

1Dコンボリューション

信号x(t)およびy(t)の線形コンボリューションは以下のように定義されます。

ここで、記号*は線形コンボリューションを意味します。

アルゴリズムがdirectの場合、VIは次の公式を使用して線形コンボリューションを個々に行い、X * Yの要素を取得します。

ここで、i = 0, 1, 2, … , M+N-2

また、h は X * Y です。

_xj = 0, j < 0, または j≥N

および

_yj ＝0、 j ＜0、または j ≧ Mとする。

アルゴリズムがfrequency domainの場合、このVIは次の手順を順に実行して線形コンボリューションを計算します。

• まず、以下の式で示すように、XとYの長さがM + N – 1となるように末尾を0でパッドします。

• 次に、以下の式に従って、X'とY'のフーリエ変換を実行します。

• さらに、X'(f)にY'(f)を乗算して、積の逆フーリエ変換を計算します。その結果が以下の式で示すようにXとYの線形コンボリューションです。

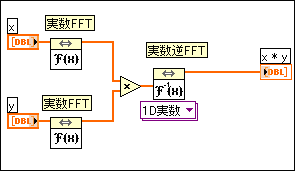
したがって、このVIは線形コンボリューションでなく巡回コンボリューションを計算します。しかし、 x(t) * y(t_)N ⇔ X(f)Y(f) はフーリエ変換の組で、 x(t) * y(t_)N は x(t) と y(t) の循環畳み込みなので、畳み込みの循環バージョンを作ることができる。巡回コンボリューションの計算には、以下の図のようなブロックダイアグラムを使用できます。

2Dコンボリューション

アルゴリズムがdirectの場合、VIは次の公式を使用して入力行列XとYの2次元コンボリューションを計算します。

ここで、i = 0, 1, 2, … , M₁+M₂–2 および j = 0, 1, 2, … , N₁+N₂–2

また、h は X * Y です。

x（m，n）、 m ＜0または m ≧_M 1または n ＜0または n ≧_N1

および

y(m,n) , m < 0 または m≥ _M2 または n < 0 または n≥ _N2.

アルゴリズムがfrequency domainの場合、VIは次の手順を順に実行して2次元コンボリューションを計算します。

• 最初に、以下の式に示すように、このVIはサイズが (M₁ + M₂ – 1) x (N₁ + N₂ – 2)となるように、XとYの末尾をゼロでパッドします。

• 次に、以下の式に従って、X'とY'のフーリエ変換を実行します。

• さらに、X'(f)にY'(f)を乗算して、積の逆フーリエ変換を計算します。その結果は、以下の式で示すようにXとYの2次元コンボリューションとなります。

出力サイズは、以下の図に示すように出力行列X * Yのサイズを指定します。

1. full

   The output matrix X * Y is (M₁+M₂–1)-by-(N₁+N₂–1).

2. size X

   画像処理を行う上で役立ちます。X がフィルタ処理する画像の場合、Y はコンボリューションカーネルと呼ばれる小さい行列です。X * Y は画像Xと同じサイズのフィルタ処理された画像です。出力サイズがfullの場合、出力M₁-x-N₁行列は、出力行列の中心部分です。

3. compact

   X * Y のエッジ要素を計算するには， 出力サイズが full または size Xの場合，ゼロパディングが必要です．LabVIEWは、出力サイズがcompactの場合、これらのエッジ要素を削除します。出力サイズがsize Xの場合、出力 (M₁–M₂+1)-x-(N₁–N₂+1) 行列は、出力行列の中心部分です。

サンプルプログラム

LabVIEWに含まれている以下のサンプルファイルを参照してください。

• labview\examples\Signal Processing\Signal Operation\Edge Detection with 2D Convolution.vi