WA Integer Wavelet Transform VI
- Updated2024-07-30
- 4 minute(s) read
Uses the lifting scheme to compute the multi-level integer wavelet transform (IWT) of signal. This VI returns the approximation coefficients at the largest level and the detail coefficients at all levels for a 1D signal input and returns the approximation coefficients and the detail coefficients at all levels for a 2D signal input. Wire data to the signal input to determine the polymorphic instance to use or manually select the instance.

WA Integer Wavelet Transform Details
Similarly to the discrete wavelet transform (DWT), this VI applies the IWT to the signal and then to the approximation coefficients of each level recursively.
On each level, this VI implements the IWT with the lifting scheme. The following illustration shows a flowchart of a one-level IWT with the lifting scheme:

al is the approximation coefficients of level l. al+1 and dl+1 are the approximation coefficients and the details coefficients of level l+1. The lifting scheme is an iterative procedure. The number of the iteration, M, depends on the wavelet type. At the first iteration, al splits into a set of even-indexed elements and a set of odd-indexed elements. This VI uses the set of even-indexed elements of the approximation coefficients of level l, al, 2k, as the initial approximation coefficients of level l+1,  . This VI uses the set of odd-indexed elements of the approximation coefficients of level l, al, 2k+1, as the initial detail coefficients of level l+1,
. This VI uses the set of odd-indexed elements of the approximation coefficients of level l, al, 2k+1, as the initial detail coefficients of level l+1,  . This VI then iteratively passes the initial approximation coefficients and the initial detail coefficients through the lifting filter, P(m)(z), and the dual lifting filter, U(m)(z), to obtain the approximation coefficients and the detail coefficients as shown in the following equations:
. This VI then iteratively passes the initial approximation coefficients and the initial detail coefficients through the lifting filter, P(m)(z), and the dual lifting filter, U(m)(z), to obtain the approximation coefficients and the detail coefficients as shown in the following equations:
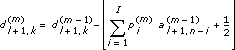

where m indicates the index of iteration, k is the coefficient index, n is the total number of coefficients, I is the number of taps of the lifting filters, and  is the operator to truncate x to the largest integer that is no greater than x. This VI computes M, P(m)(z), and U(m)(z) automatically according to the wavelet type you select.
is the operator to truncate x to the largest integer that is no greater than x. This VI computes M, P(m)(z), and U(m)(z) automatically according to the wavelet type you select.
The inverse IWT is a reverse operation of the IWT. The following illustration shows a flowchart of a one-level inverse IWT:
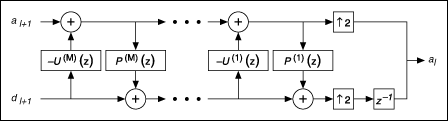
Because IWT coefficients are integers, you do not need to quantize the coefficients in the process of compression, and you do not encounter the quantization error. Therefore, the IWT and the inverse IWT are used widely in lossless signal or image compression applications.
Examples
Refer to the following VIs for examples of using the WA Integer Wavelet Transform VI:
- Lossless Medical Image Compression VI: labview\examples\Wavelet Analysis\WAApplications
- Integer Wavelet Transform on Image VI: labview\examples\Wavelet Analysis\WAGettingStarted
- Integer Wavelet Transform on 1D Signal VI: labview\examples\Wavelet Analysis\WAGettingStarted