SVD Decomposition VI

Owning Palette: Linear Algebra VIs

Requires: Multicore Analysis and Sparse Matrix Toolkit

Computes the singular value decomposition (SVD) of a matrix A.

Wire data to the A input to determine the polymorphic instance to use or manually select the instance.

Details  

SVD Decomposition (DBL)

	A specifies an m × n matrix with m rows and n columns.
	singular values only? specifies whether to compute the singular values only. The default is FALSE. If singular values only? is TRUE, this VI does not compute Matrix U and Matrix V.
	SVD option specifies how this VI performs the decomposition. 0 Thin (default)—Decomposes an m × n matrix A as the multiplication of matrix U (m × min(m,n)), S (min(m,n) × min(m,n)), and transpose of V (n × min(m,n)). 1 Full—Decomposes an m × n matrix A as the multiplication of matrix U (m × m), S (m × n), and transpose of V (n × n).
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Vector S returns the singular values of A in descending order. The values in Vector S are the diagonal elements of Matrix S.
	Matrix U returns the decomposed U matrix. The columns of Matrix U compose an orthogonal set. Matrix U is empty if singular values only? is TRUE.
	Matrix S returns the decomposed S matrix. Matrix S is a diagonal matrix whose diagonal elements are the values from Vector S, or the singular values of A in descending order.
	Matrix V returns the decomposed V matrix. The columns of Matrix V compose an orthogonal set. Matrix V is empty if singular values only? is TRUE.
	error out contains error information. This output provides standard error out functionality.

SVD Decomposition (SGL)

	A specifies an m × n matrix with m rows and n columns.
	singular values only? specifies whether to compute the singular values only. The default is FALSE. If singular values only? is TRUE, this VI does not compute Matrix U and Matrix V.
	SVD option specifies how this VI performs the decomposition. 0 Thin (default)—Decomposes an m × n matrix A as the multiplication of matrix U (m × min(m,n)), S (min(m,n) × min(m,n)), and transpose of V (n × min(m,n)). 1 Full—Decomposes an m × n matrix A as the multiplication of matrix U (m × m), S (m × n), and transpose of V (n × n).
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Vector S returns the singular values of A in descending order. The values in Vector S are the diagonal elements of Matrix S.
	Matrix U returns the decomposed U matrix. The columns of Matrix U compose an orthogonal set. Matrix U is empty if singular values only? is TRUE.
	Matrix S returns the decomposed S matrix. Matrix S is a diagonal matrix whose diagonal elements are the values from Vector S, or the singular values of A in descending order.
	Matrix V returns the decomposed V matrix. The columns of Matrix V compose an orthogonal set. Matrix V is empty if singular values only? is TRUE.
	error out contains error information. This output provides standard error out functionality.

SVD Decomposition (CDB)

	A specifies an m × n matrix with m rows and n columns.
	singular values only? specifies whether to compute the singular values only. The default is FALSE. If singular values only? is TRUE, this VI does not compute Matrix U and Matrix V.
	SVD option specifies how this VI performs the decomposition. 0 Thin (default)—Decomposes an m × n matrix A as the multiplication of matrix U (m × min(m,n)), S (min(m,n) × min(m,n)), and conjugated transpose of V (n × min(m,n)). 1 Full—Decomposes an m × n matrix A as the multiplication of matrix U (m × m), S (m × n), and conjugated transpose of V (n × n).
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Vector S returns the singular values of A in descending order. The values in Vector S are the diagonal elements of Matrix S.
	Matrix U returns the decomposed U matrix. The columns of Matrix U compose an orthogonal set. Matrix U is empty if singular values only? is TRUE.
	Matrix S returns the decomposed S matrix. Matrix S is a diagonal matrix whose diagonal elements are the values from Vector S, or the singular values of A in descending order.
	Matrix V returns the decomposed V matrix. The columns of Matrix V compose an orthogonal set. Matrix V is empty if singular values only? is TRUE.
	error out contains error information. This output provides standard error out functionality.

SVD Decomposition (CSG)

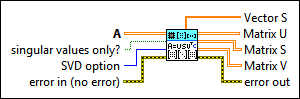
	A specifies an m × n matrix with m rows and n columns.
	singular values only? specifies whether to compute the singular values only. The default is FALSE. If singular values only? is TRUE, this VI does not compute Matrix U and Matrix V.
	SVD option specifies how this VI performs the decomposition. 0 Thin (default)—Decomposes an m × n matrix A as the multiplication of matrix U (m × min(m,n)), S (min(m,n) × min(m,n)), and conjugated transpose of V (n × min(m,n)). 1 Full—Decomposes an m × n matrix A as the multiplication of matrix U (m × m), S (m × n), and conjugated transpose of V (n × n).
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Vector S returns the singular values of A in descending order. The values in Vector S are the diagonal elements of Matrix S.
	Matrix U returns the decomposed U matrix. The columns of Matrix U compose an orthogonal set. Matrix U is empty if singular values only? is TRUE.
	Matrix S returns the decomposed S matrix. Matrix S is a diagonal matrix whose diagonal elements are the values from Vector S, or the singular values of A in descending order.
	Matrix V returns the decomposed V matrix. The columns of Matrix V compose an orthogonal set. Matrix V is empty if singular values only? is TRUE.
	error out contains error information. This output provides standard error out functionality.

SVD Decomposition Details

The following table lists the support characteristics of this VI.

Supported on RT targets	Yes
Suitable for bounded execution times on RT	Yes

Refer to the Details section in the SVD Decomposition VI for more details about this VI.