Sparse Matrix Storage Formats (Multicore Analysis and Sparse Matrix Toolkit)

Sparse matrix storage formats are a specialized data structure that stores only nonzero elements in a sparse matrix. LabVIEW supports the following sparse matrix storage formats.

• Coordinate format
• Compressed sparse row format
• Compressed sparse column format

Coordinate Format

The coordinate format (COO) is the most flexible and simplest of the sparse matrix formats. An element in a sparse matrix is represented by a triplet (row, column, element), which specifies both the coordinate and value of the element.

For example, given the following sparse matrix,

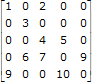
you can represent the coordinate format as follows:

The Row Indices and Column Indices specify the row and column indices of elements in the sparse matrix, respectively. Elements specifies the values of elements at the corresponding coordinate. The length of these three arrays is equal to the number of nonzeros.

The elements in the coordinate format do not need to be in a specific order. However, a sparse matrix whose elements are sorted according to their row and column indices can potentially perform better during computation. You can use the Reorder Elements VI to reorder the elements in a sparse matrix according to their row and column indices.

Compressed Sparse Row Format

The compressed sparse row format (CSR) is a variation of the coordinate format whereby the row indices are compressed. Compressing the row indices decreases memory usage. You can represent the previous sparse matrix in the compressed sparse row format as:

The length of Compressed Row Indices is the number of rows + 1. The elements in Compressed Row Indices must be in ascending order. The first element is 0 and the last element is equal to the number of nonzeros. Let r_i denote the i-th element in Compressed Row Indices. Then, the r_i-th to r_i+1-th elements in Column Indices specify the column index of elements in the i-th row in the matrix. The r_i-th to r_i+1-th elements in Elements specify the value of elements at corresponding coordinate. The length of Column Indices and Elements is equal to the number of nonzeros.

Compressed Sparse Column Format

The compressed sparse column format (CSC) is a variation of the coordinate format whereby the column indices are compressed to decrease memory usage. You can represent the previous sparse matrix in the compressed sparse column format as:

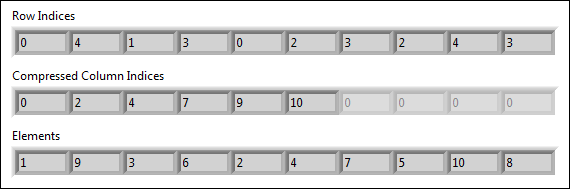
The length of Compressed Column Indices is the number of columns + 1. The elements in Compressed Column Indices must be in ascending order. The first element is 0 and the last element is equal to the number of nonzeros. Let c_i denote the i-th element in Compressed Column Indices. Then, the c_i-th to c_i+1-th elements in Row Indices specify the row index of elements in the i-th column in the matrix. The c_i-th to c_i+1-th elements in Elements specify the value of elements at corresponding coordinate. The length of Row Indices and Elements is equal to the number of nonzeros.