CD Convert Continuous Stochastic to Discrete VI

Owning Palette: Stochastic Systems VIs

Requires: Control Design and Simulation Module

Converts a continuous stochastic state-space model and the associated continuous noise model to a discrete stochastic state-space model and discrete noise model.

Details  

	Continuous Stochastic State-Space Model specifies a mathematical representation of a continuous stochastic system.
	Continuous Second-Order Statistics Noise Model specifies a continuous mathematical representation of the noise model of the Continuous Stochastic State-Space Model. A noise model defines the expected behavior of the noise vectors w and v. You can use the CD Construct Noise Model VI to construct a noise model for a given stochastic state-space system.
	Sampling Time (s) specifies the discrete sampling time of the Discrete Stochastic State-Space Model. The default value is 1 second.
	Method specifies the method this VI uses to calculate the discrete equivalent of the process noise covariance matrix Q. 0 Truncation of Taylor Series— Computes the discrete equivalent of the process noise covariance matrix by using the Truncation of Taylor Series Expansion method. 1 Numerical Integration (default)—Computes the discrete equivalent of the process noise covariance matrix by using the numerical integration method as proposed by Van Loan.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Discrete Stochastic State-Space Model returns a mathematical representation of the discrete equivalent of the Continuous Stochastic State-Space Model.
	Discrete Second-Order Statistics Noise Model returns a mathematical representation of the discrete equivalent of the Continuous Second-Order Statistics Noise Model.
	error out contains error information. This output provides standard error out functionality.

CD Convert Continuous Stochastic to Discrete Details

This VI assumes the noise vectors w and v are temporally uncorrelated. This VI also assumes the Sampling Time T you specify is much smaller than the Shannon period of the input signal u(t). Therefore, the following relationship is true:

u(t) ≈ u(kT), kT ≤ t < (k + 1)T

where t is continuous time and k is discrete time.

This VI assumes the Continuous Stochastic State-Space Model is of the following form:

This VI also assumes the Continuous Second-Order Statistics Noise Model is of the following form:

E{w(t)} = m_w(t)

E{w(t) · w^T(τ)} = Q(t) · δ(t – τ)

E{v(t)} = m_v(t)

E{v(t) · v^T(τ)} = R(t) · δ(t – τ)

E{w(t) · v^T(τ)} = N(t) · δ(t – τ)

where d(t) is the Dirac delta function. This function is defined as d(t) = ∞ when x = 0; d(t) = 0 when x ≠ 0.

This VI returns the Discrete Stochastic State-Space Model in the following form:

x[(k + 1]T] = A_dx(kT) + B_du(kT) + n(kT)

y(kT) = C_dx(kT) + D_du(kT) + r(kT), k = 0, 1, 2 ...

where

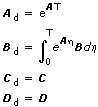
n(kT) and r(kT) are the discrete equivalents of the noise vectors.

This VI returns the Discrete Second-Order Statistics Noise Model in the following form:

E{n(kT)} = [A_d – I]A^–1Gm_w(kT)

E{n(kT) · n^T(lT)} = P(kT)δ(kT – lT), k, l = 0, 1, 2 ...

E{r(kT)} = Hm_w + m_v(kT)

E{r(kT) · r^T(lT)} = S(kT)δ(kT – lT)

E{n(kT) · r^T(lT)} = O(kT)δ(kT – lT)

where

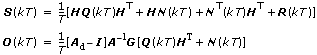
If you specify Numerical Integration for the Method parameter, then

If you specify Truncation of TSE for the Method parameter, then

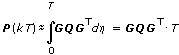
where	n is the number of states
	m is the number of inputs
	r is the number of outputs
	x is the state vector.
	u is the input vector.
	y is the output vector.
	w is the process noise vector.
	v is the observation noise vector.
	A is an n × n state matrix of the given system.
	B is an n × m input matrix of the given system.
	C is an r × n output matrix of the given system.
	D is an r × m direct transmission matrix of the given system.
	G is a matrix relating w to the states.
	H is a matrix relating w to the outputs.
	Q is the auto-covariance matrix of w.
	R is the auto-covariance matrix of v.
	N is the cross-covariance matrix between w and v.
	E{} denotes the expected mean or value of the enclosed term(s).

This approximation becomes less accurate as the value of T increases.