Determines the Jacobian elliptic functions cn, dn, and sn.


icon

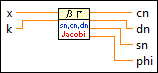
Inputs/Outputs

  • cdbl.png x —

    x is the input argument. If x is negative, the VI uses the absolute value of x.

  • cdbl.png k —

    k is the integrand parameter.

  • idbl.png cn —

    cn returns the value of the Jacobi elliptic function cn.

  • idbl.png dn —

    dn returns the Jacobi elliptic function dn.

  • idbl.png sn —

    sn returns the value of the Jacobi elliptic function sn.

  • idbl.png phi —

    phi is the upper limit of the integral defining the function.

    • The following equations define the three Jacobian elliptic functions.

    cn(x, k) = cos(ϕ) sn(x, k) = sin(ϕ)

    where

    The function is defined according to the following intervals for the input values.

    For any real value of integrand parameter k in the unit interval, the function is defined for all real values of x.