Defines the right side of a partial differential equation and its coefficients. You must manually select the polymorphic instance to use.


icon

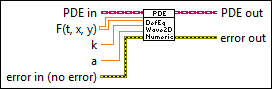
Inputs/Outputs

  • cNI__PDE_lvlib_NI__PDElvclass.png PDE in —

    PDE in is the class that stores the data of the equation.

  • c3ddbl.png F(t, x, y) —

    F(t, x, y) specifies the value of the right side of the equation.

    The size of the right side of the equation must be # of t-points-by-# of y-points-by-# of x-points from the Define PDE Domain VI. Each page of F(t, x, y) stores the value of the right side of the equation evaluated on mesh grid points (X, Y) from the Define PDE Domain VI at a particular time step. On one page of F(t, x, y), each row or column stores the values of the right side of the equation evaluated on a particular y- or x-point. By default, LabVIEW assumes the values of F(t, x, y) are zeros.

  • cdbl.png k —

    k is a squared value that specifies the coefficient of the second order partial derivative of the unknown function in the equation. k cannot be 0. The default is 1.

  • cdbl.png a —

    a specifies the coefficient of the unknown function in the equation. The default is 0.

  • cerrcodeclst.png error in (no error) —

    error in describes error conditions that occur before this node runs. This input provides standard error in functionality.

  • iNI__PDE_lvlib_NI__PDElvclass.png PDE out —

    PDE out returns the right side of PDE in and its coefficients.

  • ierrcodeclst.png error out —

    error out contains error information. This output provides standard error out functionality.

    • Helmholtz Equation

    The following equation defines the Helmholtz equation:

    where k and a are constant coefficients, u is the unknown function, and f is the right side of the equation. The operator is the Laplacian. The Laplacian in Cartesian coordinates is defined as

    in two-dimensional space and

    in three-dimensional space.

    Heat Equation

    The following equation defines the general form of the heat equation:

    Wave Equation

    The following equation defines the general form of the wave equation:

    Examples

    Refer to the following example files included with LabVIEW.

    • labview\examples\Mathematics\Differential Equations - PDE\PDE Flexible Element.vi
    • labview\examples\Mathematics\Differential Equations - PDE\PDE String Vibration.vi
    • labview\examples\Mathematics\Differential Equations - PDE\PDE Thermal Distribution.vi