The adaptive spectrogram method shares similarities with the Gabor spectrogram method, differing in their respective signal decomposition techniques.

The adaptive spectrograms utilize adaptive expansion for signal decomposition, while Gabor spectrograms employ Gabor expansion. Both methods apply the Wigner-Ville Distribution (WVD). However, the adaptive spectrogram selectively sums WVD contributions from individual functions (auto-terms), excluding cross-terms between pairs of functions.

The adaptive spectrogram has a fine and adaptive time-frequency resolution because the elementary functions of the adaptive expansion have a fine and adaptive time-frequency resolution. The time-frequency resolution of the adaptive transform adapts to the signal characteristics. The adaptive spectrogram does not include cross-term interference because it ignores all the cross-terms. For example, if a signal is composed of chirplets, you can use the adaptive spectrogram to depict accurately how the chirplets appear in the time-frequency domain.

The computation time of the adaptive spectrogram increases with the size of the data set. Also, if the signal has a nonlinear frequency modulation, the adaptive spectrogram might include too much distortion because the adaptive expansion approximates the nonlinear modulation as a linear combination of chirplets with linear frequency modulation.

Use the TFA Adaptive Spectrogram VI to compute the adaptive spectrogram.

The following figure shows twenty superimposed, simulated chirplets designed to test the time-frequency resolution and performance of the adaptive spectrogram. You cannot distinguish the separate chirplets in the time-domain representation in the following figure:

Figure 41. Time-Domain Representation of Twenty Simulated Chirplets

The following figure shows the adaptive spectrogram of the simulated chirplet signal in the previous figure:

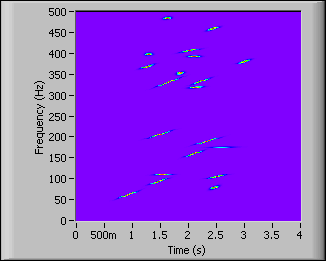
Figure 42. Adaptive Spectrogram of Twenty Simulated Chirplets

All the chirplets in the previous figure are separated clearly, appear compact, and show that the adaptive spectrogram has a high and adaptive time-frequency resolution.

The following figure shows the Gabor spectrogram of the simulated chirplet signal when the order is 2 and the window length is 256:

Figure 43. Gabor Spectrogram of a Simulated Chirplet Signal
  • 1—Blended Chirplets

    • The Gabor spectrogram in the previous figure has a lower time-frequency resolution than the adaptive spectrogram in the figure of the adaptive spectrogram of the simulated chirplet signal, and some of the chirplets blend together, which prevents you from separating the two signal components.