WA Analytic Wavelet Transform VI

Owning Palette: Continuous Wavelet VIs

Requires: Advanced Signal Processing Toolkit

Uses the complex-valued Morlet wavelet to compute the continuous wavelet transform (CWT) of a 1D input signal. Wire data to the signal input to determine the polymorphic instance to use or manually select the instance.

The analytic wavelet transform (AWT) also is known as the complex wavelet transform.

Details  Examples

WA Analytic Wavelet Transform (Waveform)

	normalization specifies how to scale the dilated wavelets. 0 energy (default)—Specifies that the wavelets have a unified energy in all scales. 1 amplitude—Specifies that wavelets at different scales have the same maximum amplitude of frequency response.
	time steps specifies the number of samples to translate, or shift, the wavelet in the analytic wavelet transform (AWT). The default is –1, which specifies that this VI adjusts time steps automatically so that no more than 512 coefficients exist at each scale. The number of rows in the output wavelet coefficients equals the signal length divided by time steps. National Instruments recommends that you set time steps such that the number of rows in the wavelet coefficients does not exceed 512. If you specify a small value for time steps, this VI might return a large number of wavelet coefficients, which requires a long computation time and more memory. If you need a small time step to observe more details and the signal length is large, divide the signal into smaller segments and compute the wavelet coefficients for each segment. If the signal is oversampled, you can downsample the signal. time steps must be greater than 0, or this VI sets time steps to the default value –1 automatically.
	signal specifies the input signal.
	scales specifies the number of scales of the dilated wavelet.
	scale sampling method specifies the method to use to select the scales of the wavelets. scale sampling method affects the mapping style of the y-axis of the scalogram. Use the user defined scales input to specify a customized scale. 0 even frequency (default)—This VI computes the continuous wavelet transform (CWT) such that the center frequencies of the wavelets at the analyzed scales evenly sample the frequency range from 0 to sampling rate/2. The central frequency of a wavelet is inversely proportional to the scale. The resulting scalogram is a kind of joint time-frequency representation with an adaptive time-frequency resolution. 1 even scale—This VI computes the CWT at positive integer scales 1, 2, 3, ..., scales.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	user defined scales specifies the scales to use to compute AWT coef. The scale must be positive and no greater than the length of signal. If you specify a value for user defined scales, this VI ignores the settings in the scale sampling method input and the scales input.
	AWT coef returns the results of the analytic wavelet transform (AWT). The element in the ith column and the jth row is the result of the AWT at the (i+1)th scale with a translation of j×time steps. When you use user defined scales to define the scales of the AWT, the element in the ith column and the jth row is the result of the AWT, where scale (a) equals the ith element of user defined scales and shift () equals j×time steps. The squared magnitude of AWT coef is the scalogram, which jointly represents a signal in terms of time and scale. Large scales correspond to low frequencies, and small scales correspond to high frequencies. Use the WA Scalogram Indicator to display the scalogram on an intensity graph.
	scale info returns the time information and the scale (frequency) information, which this VI uses in the scalogram plot.
	error out contains error information. This output provides standard error out functionality.

WA Analytic Wavelet Transform (Array)

	normalization specifies how to scale the dilated wavelets. 0 energy (default)—Specifies that the wavelets have a unified energy in all scales. 1 amplitude—Specifies that wavelets at different scales have the same maximum amplitude of frequency response.
	time steps specifies the number of samples to translate, or shift, the wavelet in the analytic wavelet transform (AWT). The default is –1, which specifies that this VI adjusts time steps automatically so that no more than 512 coefficients exist at each scale. The number of rows in the output wavelet coefficients equals the signal length divided by time steps. National Instruments recommends that you set time steps such that the number of rows in the wavelet coefficients does not exceed 512. If you specify a small value for time steps, this VI might return a large number of wavelet coefficients, which requires a long computation time and more memory. If you need a small time step to observe more details and the signal length is large, divide the signal into smaller segments and compute the wavelet coefficients for each segment. If the signal is oversampled, you can downsample the signal. time steps must be greater than 0, or this VI sets time steps to the default value –1 automatically.
	signal specifies the input signal.
	scales specifies the number of scales of the dilated wavelet.
	scale sampling method specifies the method to use to select the scales of the wavelets. scale sampling method affects the mapping style of the y-axis of the scalogram. Use the user defined scales input to specify a customized scale. 0 even frequency (default)—This VI computes the continuous wavelet transform (CWT) such that the center frequencies of the wavelets at the analyzed scales evenly sample the frequency range from 0 to sampling rate/2. The central frequency of a wavelet is inversely proportional to the scale. The resulting scalogram is a kind of joint time-frequency representation with an adaptive time-frequency resolution. 1 even scale—This VI computes the CWT at positive integer scales 1, 2, 3, ..., scales.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	user defined scales specifies the scales to use to compute AWT coef. The scale must be positive and no greater than the length of signal. If you specify a value for user defined scales, this VI ignores the settings in the scale sampling method input and the scales input.
	sampling rate specifies the sampling rate of signal in hertz. sampling rate must be greater than 0, or this VI sets sampling rate to 1 automatically. The default is 1.
	AWT coef returns the results of the analytic wavelet transform (AWT). The element in the ith column and the jth row is the result of the AWT at the (i+1)th scale with a translation of j×time steps. When you use user defined scales to define the scales of the AWT, the element in the ith column and the jth row is the result of the AWT, where scale (a) equals the ith element of user defined scales and shift () equals j×time steps. The squared magnitude of AWT coef is the scalogram, which jointly represents a signal in terms of time and scale. Large scales correspond to low frequencies, and small scales correspond to high frequencies. Use the WA Scalogram Indicator to display the scalogram on an intensity graph.
	scale info returns the time information and the scale (frequency) information, which this VI uses in the scalogram plot.
	error out contains error information. This output provides standard error out functionality.

WA Analytic Wavelet Transform Details

The AWT is a special case of the CWT with the complex-valued Morlet wavelet, also called the Gabor wavelet. The following equation defines the complex-valued Morlet wavelet:

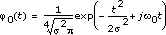
where is the standard deviation of the Gaussian envelope of the mother wavelet, and is the central frequency of the mother wavelet, which is in this VI.

Scale and Frequency

The following illustration shows the real parts of the complex-valued Morlet wavelet. The scales and shifts, (a, ), are (16, 100), (32, 200), and (64, 300) respectively.

The following illustration shows the Fourier transforms of the previous complex-valued Morlet wavelet:

From the above illustrations, you can see that the center frequency of the scaled wavelet is inversely proportional to the scale a.

The Fourier transform of is , where is the Fourier transform of the mother wavelet. Therefore, the center frequency of the scaled wavelet is . You can use the AWT to analyze the frequency content of a signal by selecting a set of scales.

Examples

Refer to the following VIs for examples of using the WA Analytic Wavelet Transform VI:

• Scalogram with Analytic Wavelet Transform VI: labview\examples\Wavelet Analysis\WAGettingStarted
• Spectrogram Ridge Detection VI: labview\examples\Wavelet Analysis\WAGettingStarted
• Color Tables for Displaying the Scalogram VI: labview\examples\Wavelet Analysis\WAGettingStarted