Estimating Gaussian Chirplet and Gaussian Pulse (Advanced Signal Processing Toolkit)

You can consider the elementary functions that the discrete Gabor expansion uses, such as Gaussian-windowed, complex-sinusoid functions or complex, frequency-modulated Gaussian functions, as being a set of time-shifted and frequency-modulated versions of a single prototype function.

The following equation represents the linear Gaussian chirplet:

where	is the time-frequency center of the chirplet
	is the standard deviation of the Gaussian envelope
	is the chirp rate

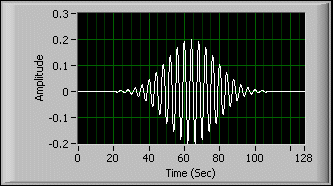
The following figures show the time waveform and the time-frequency spectrogram of the Gaussian chirplet:

Use the TFA Adaptive Transform VI to select either Gaussian chirplet or Gaussian pulse as the elementary function to represent a signal. When you choose the Gaussian pulse in the elementary functions, this VI forces the chirp rate to 0. The following illustrations show the waveform and the time-frequency spectrogram of the linear Gaussian pulse in this situation:

Given a signal, s(t), the adaptive transform computes the parameters of each elementary function by using the matching pursuit method together with a fast refinement algorithm.

When you specify how many possible terms of Gaussian chirplet or Gaussian pulse exist for the signal, the TFA Adaptive Transform VI estimates the parameters of the Gaussian chirplets or the Gaussian pulses. The estimated Gaussian chirplets or Gaussian pulses can be distributed in the time-frequency domain arbitrarily. The time and the frequency centers of the Gaussian chirplets or Gaussian pulses are not fixed in a grid. Also, the envelopes of the Gaussian chirplets or Gaussian pulses are arbitrary. In comparison, the discrete Gabor expansion has a fixed sampling grid and a fixed envelope for all the elementary functions.