Reelle Laplace-Transformation
- Aktualisiert2025-07-30
- 3 Minute(n) Lesezeit
Berechnet die reelle Laplace-Transformation der Eingangsfolge X.

Ein-/Ausgänge
 X
—
X
—
X ist das Array, das das gleichmäßig abgetastete Zeitsignal beschreibt. Das erste Element dieses Arrays gehört zu t = 0, das letzte zu t = Ende.  Ende
—
Ende
—
Ende ist der Zeitwert des letzten Samples. Das gesamte Sample-Intervall liegt zwischen 0 und Ende.  Laplace {X}
—
Laplace {X}
—
Laplace {X} ist das Ergebnis der Laplace-Transformation in Form eines Arrays.  Fehler
—
Fehler
—
Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode. |
Die reelle Laplace-Transformation eines reellen Signals x(s) ist wie folgt definiert:
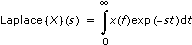
für s ≥ 0 und s real.
Hier ist x(t) definiert für alle: t ≥ 0.
Die diskrete Version der Laplace-Transformation eines diskret und gleichmäßig abgetasteten Signals ist eine Ableitung der oben beschriebenen, kontinuierlichen Version.
Die Laplace-Transformation ist ungeeignet in Fällen, in denen das Zeitsignal schnell ansteigt. Mit der diskreten Laplace-Transformation kann die Konvergenz nicht in gleicher Weise bestimmt werden wie mit der ursprünglichen Definition.
Zudem ist der Berechnungsaufwand bei der diskreten Version der Laplace-Transformation sehr groß. Eine effiziente Methode für die diskrete Laplace-Transformation beruht auf der schnellen partiellen Fourier-Transformation (FFFT). Die Definition der FFFT lautet wie folgt:
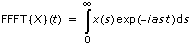
mit einem beliebig ausgewählten komplexen Wert α.
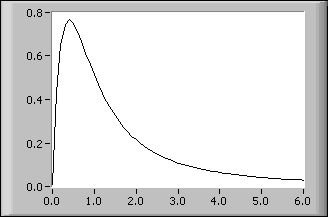
Im folgenden Diagramm sehen Sie die reelle Laplace-Transformation der Funktion f(t) = sin(t) im Intervall (0, 6). Dies wird auf der Frontplatte als Ende 6.00 und X-Werte von sin(t) für 0 ≤ t ≤ 6 eingegeben.