Berechnet den linearen Korrelationskoeffizienten zwischen den Eingangsfolgen X und Y.


icon

Ein-/Ausgänge

  • c1ddbl.png X —

    X ist die erste Eingangsfolge.

  • c1ddbl.png Y —

    Y ist die zweite Eingangsfolge.

  • idbl.png Korrelationskoeffizient r —

    Korrelationskoeffizient r gibt den Korrelationskoeffizienten zwischen X und Y aus.

  • idbl.png r^2 —

    r^2 gibt das Quadrat von Korrelationskoeffizient r aus.

    • Der lineare Korrelationskoeffizient wird auch als Produkt-Moment-Koeffizient der Korrelation oder als Pearson-Korrelation bezeichnet. Die folgende Gleichung beschreibt den linearen Korrelationskoeffizienten:

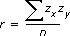
    wobei zx und zy die standardisierten z-Werte von X und Y sind. Die standardisierten z-Werte kennzeichnen, wie viele Standardabweichungen X und Y über bzw. unter dem Mittelwert liegen.

    Der Korrelationskoeffizient r liegt immer im Intervall [–1, 1]. Wenn der Korrelationskoeffizient r 1 ist, besteht zwischen X und Y eine vollständige positive Korrelation. Anders ausgedrückt: Die Datenwerte von X und Y liegen auf einer perfekten, ansteigenden Geraden. Wenn der Korrelationskoeffizient r –1 ist, besteht zwischen X und Y eine vollständige negative Korrelation. Anders ausgedrückt: Die Datenwerte von X und Y liegen auf einer perfekten, abfallenden Geraden. Wenn der Korrelationskoeffizient r 0 ist, besteht zwischen X und Y keine Korrelation.