Sphärische Hankel-Funktion hn

PDF herunterladen

Berechnet die sphärische Hankel-Funktion, die auch als sphärische Bessel-Funktion dritter Art bezeichnet wird.

Ein-/Ausgänge

x —

x ist das Eingangsargument. Bei einem negativen n wird der absolute Wert von x verwendet.

n —

n gibt die Ordnung der sphärischen Hankel-Funktion an.

Typ —

Typ gibt den Typ der Hankel-Funktion an.


0	Erste Art—Berechnet die sphärische Hankel-Funktion erster Art.
1	Zweite Art—Berechnet die sphärische Hankel-Funktion zweiter Art.

hn(x) —

hn(x) gibt den Wert der sphärischen Hankel-Funktion aus.

Die sphärische Hankel-Funktion erster Art der Ordnung n wird nach folgender Gleichung berechnet:

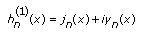
Die sphärische Hankel-Funktion zweiter Art der Ordnung n wird nach folgender Gleichung berechnet:

wobei j_n eine sphärische Bessel-Funktion erster Art und y_n eine sphärische Bessel-Funktion zweiter Art ist.

Die sphärische Hankel-Funktion ist durch folgende Intervalle für die Eingangswerte gekennzeichnet:

Zu jedem ganzzahligen Wert der Ordnung n unterstützt LabVIEW nicht negative reelle Werte von x.