Bestimmt die Ellipsenfunktionen nach Jacobi cn, dn und sn.


icon

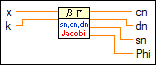
Ein-/Ausgänge

  • cdbl.png x —

    x ist das Eingangsargument. Bei einem negativen n wird der absolute Wert von x verwendet.

  • cdbl.png k —

    k ist der Integrand.

  • idbl.png cn —

    cn gibt den Wert der Ellipsenfunktion nach Jacobi cn aus.

  • idbl.png dn —

    dn gibt die Ellipsenfunktion nach Jacobi dn aus.

  • idbl.png sn —

    sn gibt den Wert der Ellipsenfunktion nach Jacobi sn aus.

  • idbl.png Phi —

    phi ist der obere Grenzwert des Integrals, das die Funktion bestimmt.

    • Folgende Gleichungen beschreiben die drei Ellipsenfunktionen nach Jacobi:

    cn(x, k) = cos(ϕ) sn(x, k) = sin(ϕ)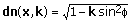

    wobei

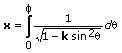
    Die Funktion ist für die folgenden Intervalle von Eingangswerten definiert:

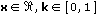
    Für jeden reellen Wert des Integranden k im Einheitsintervall ist die Funktion für alle reellen Werte von x definiert.