Löst anhand des Runge-Kutta-Verfahrens gewöhnliche Differentialgleichungen mit Anfangsbedingungen.


icon

Ein-/Ausgänge

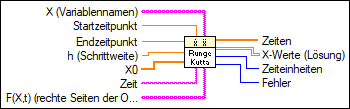
  • c1dstr.png X (Variablennamen) —

    X ist ein Array aus Variablen-Strings.

  • cdbl.png Startzeitpunkt —

    Startzeitpunkt ist der Startpunkt der gewöhnlichen Differentialgleichung. Der Standardwert lautet 0.

  • cdbl.png Endzeitpunkt —

    Endzeitpunkt ist der Endpunkt des Zeitintervalls, das untersucht werden soll. Der Standardwert lautet 1,0.

  • cdbl.png h (Schrittweite) —

    h ist die unveränderliche Schrittweite. Die Standardeinstellung lautet 0,1.

  • c1ddbl.png X0 —

    X0 ist der Vektor der Anfangsbedingung x[10], …, x[n0].

    Zwischen X0 und X besteht eine eineindeutige Beziehung.

  • cstr.png Zeit —

    Zeit ist der String zur Angabe der Zeitvariable. Die Standardvariable lautet t.

  • c1dstr.png F(X,t) (rechte Seiten der ODE als Funktionen von X und t) —

    F(X,t) ist ein Array mit Strings, die die rechten Seiten der Differentialgleichungen darstellen. Die Formeln können beliebig viele gültige Variablen enthalten.

  • i1ddbl.png Zeiten —

    Zeitwerte ist ein Array, das die Zeitschritte darstellt. Beim Runge-Kutta-Verfahren werden äquidistante Zeitschritte zwischen Startzeitpunkt und Endzeitpunkt verwendet.

  • i2ddbl.png X-Werte (Lösung) —

    X-Werte ist ein 2D-Array des Lösungsvektors x[10], …, x[n].

    Der obere Index durchläuft die Zeitschritte, die im Array Zeiten festgelegt sind, und der untere Index die Elemente x[10], …, x[n].

  • iu32.png Zeiteinheiten —

    Zeiteinheiten entspricht dem Zeitaufwand für die gesamte Berechnung in Millisekunden.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Fehler können durch falsche Eingaben für X, X0 und F(X,t) entstehen. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Die Runge-Kutta-Methode der 4. Ordnung arbeitet mit einem höheren Genauigkeitsgrad als das häufig verwendete Euler-Verfahren mit unveränderlicher Schrittweite (5-stufiger Prozess), genauer:

    und

    mit .

    Die Methode endet wenn

    tn ≥ Zeitende.

    In der Abbildung wird die Lösung des folgenden gewöhnlichen Differentialgleichungssystems angezeigt:

    Geben Sie auf dem Frontpanel die folgenden Gleichungen ein:

    • Startzeitpunkt: 0,00
    • Endzeitpunkt: 20,00
    • X: [x, y, z]
    • X0: [1, 1, 1]
    • F(X,t): [10*(y – x), x*(28 – z) – y, x*y – (8/3)*z]

    Hinweis Obwohl eigentlich drei Lösungen existieren, zeigt ein Blick auf die Kurve, dass scheinbar nur zwei Lösungen existieren. Der Grund dafür ist, dass die Lösungen für x und y sehr ähnlich sind, so dass sie sich fast überlappen.

    Beispiele

    Die folgenden Beispieldateien sind in LabVIEW enthalten.

    • labview\examples\Mathematics\Differential Equations - ODE\Shooting Method.vi
    • labview\examples\Mathematics\Differential Equations - ODE\Process Control Explorer.vi