Löst ein n-dimensionales lineares Differentialgleichungssystem mit gegebener Anfangsbedingung. Die Lösung basiert auf der Bestimmung der Eigenwerte und Eigenvektoren der zugrunde liegenden Matrix und wird in symbolischer Form angezeigt.


icon

Ein-/Ausgänge

  • c2ddbl.png A (Koeffizientenmatrix) —

    A ist die (n, n)-Matrix, mit der das lineare System beschrieben wird.

  • c1ddbl.png X0 (Startwert) —

    X0 ist der Vektor n zur Beschreibung der Anfangsbedingung x[10], …, x[n0].

    Zwischen X0 und X besteht eine eineindeutige Beziehung.

  • istr.png Formel —

    Formel ist ein String mit der Lösung des linearen Systems in der Standard-Formelschreibweise von LabVIEW. Die Elemente des Lösungsvektors sind durch Wagenrückläufe voneinander getrennt.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Fehler können durch falsche Eingaben für X, X0 und F(X,t) entstehen. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Hinweis Dieses VI arbeitet bei reellen Matrizen A in fast allen Fällen problemlos. Die Matrizen können also auch auch doppelte oder komplex konjugierte Eigenwerte enthalten. Die Ausnahme bildet eine singuläre Eigenvektormatrix, das heißt eine Matrix, bei der die Eigenvektoren nicht den gesamten Raum aufspannen. Wenn die Eigenvektor-Matrix singulär ist, wird ein Fehler von -23016 angezeigt.

    Die lineare Differentialgleichung, die durch das folgende System beschrieben wird:

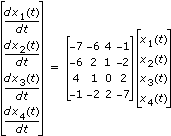
    mit

    x1(0) = 1 x2(0) = 2 x3(0) = 3 x4(0) = 4

    hat die Lösung:

    + 1,62*e(-12,46*t) - 1,28*e(-6,30*t) + 0,63*e(1,34*t) + 0,04*e(5,42*t) + 0,84*e(-12,46*t) - 0,29*e(-6,30*t) + 1,51*e(1,34*t) - 0,06*e(5,42*t) -0,73*E(-12,46*t) + 0,01*E(-6,30*t) + 3,69*E(1,34*t) + 0,02*E(5,42*t) + 0,87*E(-12,46*t) + 2,67*E(-6,30*t) + 0,45*E(1,34*t) + 0,01*E(5,42*t)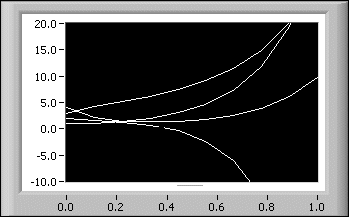

    In der nachfolgenden Parameterliste sehen Sie, wie die Gleichung auf dem Frontpanel einzugeben ist:

    • A: [–7, –6, 4, 1; –6, 2, 1, –2; 4, 1, 0, 2; –1, –2, 2, –7]
    • X0: [1, 2, 3, 4]