Löst ein n-dimensionales homogenes lineares Differentialgleichungssystem mit konstanten Koeffizienten und gegebener Anfangsbedingung.


icon

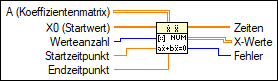
Ein-/Ausgänge

  • c2ddbl.png A (Koeffizientenmatrix) —

    A ist die (n, n)-Matrix, mit der das lineare System beschrieben wird.

  • c1ddbl.png X0 (Startwert) —

    X0 ist der Vektor n zur Beschreibung der Anfangsbedingung x[10], …, x[n0].

    Zwischen X0 und X besteht eine eineindeutige Beziehung.

  • cu32.png Werteanzahl —

    Werteanzahl ist die Anzahl der äquidistanten Zeitwerte zwischen Startzeitpunkt und Endzeitpunkt. Der Standardwert lautet 10.

  • cdbl.png Startzeitpunkt —

    Startzeitpunkt ist der Startpunkt der gewöhnlichen Differentialgleichung. Der Standardwert lautet 0.

  • cdbl.png Endzeitpunkt —

    Endzeitpunkt ist der Endpunkt des Zeitintervalls, das untersucht werden soll. Der Standardwert lautet 1,0.

  • i1ddbl.png Zeiten —

    Zeitwerte ist ein Array, das die Zeitschritte darstellt. Beim Euler-Verfahren werden dieselben Zeitschritte zwischen Startzeitpunkt und Endzeitpunkt verwendet.

  • i2ddbl.png X-Werte —

    X-Werte ist die Matrix der Lösung X an den äquidistanten Zeitpunkten.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Fehler können durch falsche Eingaben für X, X0 und F(X,t) entstehen. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Die Lösung des VIs basiert auf der Bestimmung der Eigenwerte und -vektoren der zugrundeliegenden Matrix A und wird in Form von Zahlenwerten angezeigt.

    Hinweis Dieses VI arbeitet bei reellen Matrizen A in fast allen Fällen problemlos. Die Matrizen können also auch auch doppelte oder komplex konjugierte Eigenwerte enthalten. Die Ausnahme bildet eine singuläre Eigenvektormatrix, das heißt eine Matrix, bei der die Eigenvektoren nicht den gesamten Raum aufspannen. Wenn die Eigenvektor-Matrix singulär ist, wird ein Fehler von -23016 angezeigt.

    Lineare Systeme können wie folgt beschrieben werden:

    X(0) = X0

    bei Startzeitpunkt= 0.

    Hier gilt:

    X(t) = (x0(t), …, xn(t))

    und A ist eine reelle (n, n)-Matrix. Das lineare System kann durch Bestimmen der Eigenwerte und -vektoren von A gelöst werden. S steht für alle Eigenvektoren, die über den gesamten n-dimensionalen Bereich aufgespannt sind. Durch die Transformation Y(t) = SX(t) ergibt sich

    Y(0) = SX0

    Die Matrix SAS–1 ist diagonal, daher liegt die Lösung auf der Hand. Die Lösung X(t) kann durch Rücktransformation bestimmt werden:

    X(t) = S–1Y(t)
    Hinweis Die Zeit wird nicht ausgegeben, da das Hauptanliegen darin besteht, die Eigenvektoren und Eigenwerte der Matrix A zu bestimmen. Bei relativ kleinen Dimensionen von A kann dieser Vorgang vernachlässigt werden.

    In folgender Abbildung sind die vier Komponenten der Lösung der linearen Differentialgleichung dargestellt, die durch das folgende System beschrieben wird:

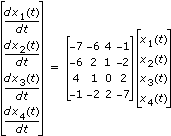
    mit

    x1(0) = 1 x2(0) = 2 x3(0) = 3 x4(0) = 4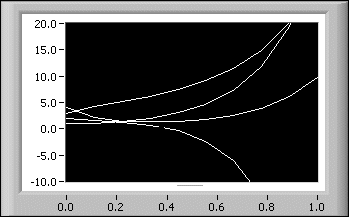

    In der nachfolgenden Parameterliste sehen Sie, wie die Gleichung auf dem Frontpanel einzugeben ist:

    • A: [–7, –6, 4, 1; –6, 2, 1, –2; 4, 1, 0, 2; –1, –2, 2, –7]
    • X0: [1, 2, 3, 4]
    • Startzeitpunkt: 0,00
    • Endzeitpunkt: 1,00