Löst mit dem Euler-Verfahren gewöhnliche Differentialgleichungen mit Anfangsbedingungen.


icon

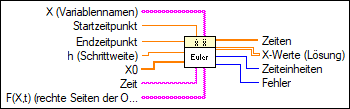
Ein-/Ausgänge

  • c1dstr.png X (Variablennamen) —

    X ist ein Array aus Variablen-Strings.

  • cdbl.png Startzeitpunkt —

    Startzeitpunkt ist der Startpunkt der gewöhnlichen Differentialgleichung. Der Standardwert lautet 0.

  • cdbl.png Endzeitpunkt —

    Endzeitpunkt ist der Endpunkt des Zeitintervalls, das untersucht werden soll. Der Standardwert lautet 1,0.

  • cdbl.png h (Schrittweite) —

    h ist die unveränderliche Schrittweite. Die Standardeinstellung lautet 0,1.

  • c1ddbl.png X0 —

    X0 ist der Vektor der Anfangsbedingung x[10], …, x[n0].

    Zwischen X0 und X besteht eine eineindeutige Beziehung.

  • cstr.png Zeit —

    Zeit ist der String zur Angabe der Zeitvariable. Die Standardvariable lautet t.

  • c1dstr.png F(X,t) (rechte Seiten der ODE als Funktionen von X und t) —

    F(X,t) ist ein Array mit Strings, die die rechten Seiten der Differentialgleichungen darstellen. Die Formeln können beliebig viele gültige Variablen enthalten.

  • i1ddbl.png Zeiten —

    Zeitwerte ist ein Array, das die Zeitschritte darstellt. Beim Euler-Verfahren werden zwischen Startzeitpunkt und Endzeitpunkt gleich große Zeitschritte verwendet.

  • i2ddbl.png X-Werte (Lösung) —

    X-Werte ist ein 2D-Array des Lösungsvektors x[10], …, x[n].

    Der obere Index durchläuft die Zeitschritte, die im Array Zeiten festgelegt sind, und der untere Index die Elemente x[10], …, x[n].

  • iu32.png Zeiteinheiten —

    Zeiteinheiten entspricht dem Zeitaufwand für die gesamte Berechnung der Funktionswerte in Millisekunden.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Fehler können durch falsche Eingaben für X, X0 und F(X,t) entstehen. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Die allgemeine Form einer gewöhnlichen Differentialgleichung lautet:

    mit

    Die Funktionen f1, …, fn, die Anzahl und der Startpunkt t = t0 sind gegeben. Mit der Vorgabe F = (f1, …, fn); X(t) = (x1(t), …, xn(t)) und X0 = (x10, …, xn0),

    gilt:

    Es müssen die Funktionen X bestimmt werden, die die obigen Gleichungen erfüllen.

    Das Euler-Verfahren ist ein Standardverfahren, anhand dessen gewöhnliche Differentialgleichungen gelöst werden können. Ausgehend von t0 und einer unveränderlichen Schrittweite h (die im Allgemeinen relativ klein ist) werden die neuen Werte

    X(t0 + h) = X(t0) +hF(X(t0), t) X(t0 +2h) = X(t0 + h) +hF(X(t0 + h),t0 + h) ⋮

    berechnet. Dieser Prozess endet, wenn Zeitbeginn +nh ≥ Zeitende, wobei Zeitende der rechte Endpunkt des untersuchten Zeitintervalls ist.

    In der Abbildung wird die Lösung der folgenden gewöhnlichen Differentialgleichung angezeigt.

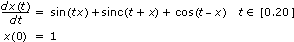
    Die Gleichung und die Anfangsbedingung sind wie folgt auf dem Frontpanel einzugeben:

    • Startzeitpunkt: 0,00
    • Endzeitpunkt: 20,00
    • X0: 1,00
    • F(X,t): sin(t*x) + sinc(t + x) + cos(t – x)
    • X: x