Bestimmt anhand des Levenberg-Marquardt-Algorithmus die Parameter, die die Eingangspaare (X, Y) und damit eine nichtlineare Funktion des Typs y = f(x,a) am besten erfüllen (a sind die Parameter). Die polymorphe Instanz muss manuell ausgewählt werden.


icon

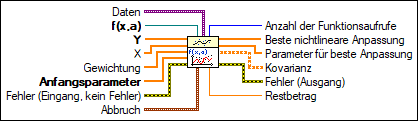
Ein-/Ausgänge

  • cfxdt.png Daten —

    Daten enthält statische Daten, die von der benutzerdefinierten Funktion während der Ausführung benötigt werden.

  • csvrn.png f(x,a) —

    f(x,a) ist eine Referenz auf das VI, mit dem das Anpassungsmodell implementiert wird. a sind die von LabVIEW berechneten Parameter.

    Verwenden Sie die VI-Vorlage, die sich unter labview\vi.lib\gmath\NumericalOptimization\LM model function und gradient.vit befindet, um das VI anhand einer Vorlage zu erstellen.

  • c1ddbl.png Y —

    Y ist das Array mit den abhängigen Werten oder den Beobachtungswerten. Die Anzahl der Eingangspunkte muss größer 0 sein.

  • c1ddbl.png X —

    X ist das Array mit den unabhängigen Werten. Die Anzahl der Eingangspunkte muss größer 0 sein.

  • c1ddbl.png Gewichtung —

    Gewichtung ist ein Array mit den Gewichtungen für die Beobachtungswerte Y. Wenn Gewichtung offen gelassen wird, werden alle Elemente von Gewichtung automatisch auf 1 gesetzt.

    Wenn Gewichtung weniger Elemente als Y enthält, füllt dieses VI das Ende von Gewichtung mit Einsen auf, so dass die Länge von Gewichtung der Länge von Y entspricht. Wenn Gewichtung mehr Elemente als Y enthält, ignoriert das VI die zusätzlichen Elemente am Ende von Gewichtung. Bei Elementen kleiner als 0 wird mit dem Absolutwert gearbeitet.

  • c1ddbl.png Anfangsparameter —

    Anfangsparameter gibt die vermutete Lösung für Parameter für beste Anpassung an. Die Länge von Anfangsparameter muss der Länge von a in f(x,a) entsprechen.

    Der Erfolg einer nicht linearen Kurvenanpassung hängt davon ab, wie nah die Anfangsparameter an Parameter für beste Anpassung liegen. Daher sollten Sie vor Anwendung dieses VIs alle zur Verfügung stehenden Quellen verwenden, um möglichst genaue Anfangsparameter für die Schätzung zu erhalten.

  • cerrcodeclst.png Fehler (Eingang, kein Fehler) —

    Fehler (Eingang) beschreibt Fehlerbedingungen, die vor der Ausführung des Knotens auftreten. An Fehler (Eingang) werden Standardfehlerdaten übergeben.

  • cnclst.png Abbruch —

    Abbruch gibt die Bedingungen für den Abbruch des Anpassungsprozesses an.

  • ci32.png Max. Iterationen —

    Max. Iterationen ist die größte Anzahl an Iterationen der Anpassungsroutine. Wenn die Anzahl der Iterationen Max. Iterationen überschreitet, wird der Anpassungsprozess abgebrochen.

  • cdbl.png Toleranz —

    Toleranz ist die relative Änderung im gewichteten Abstand zwischen Y und der aktuellen Anpassung. Wenn die relative Änderung unter die Toleranz fällt, wird der Anpassungsprozess abgebrochen.

  • ii32.png Anzahl der Funktionsaufrufe —

    Anzahl der Funktionsaufrufe gibt an, wie oft f(x,a) während des Anpassungsprozesses aufgerufen wurde.

  • i1ddbl.png Beste nichtlineare Anpassung —

    Beste nichtlineare Anpassung gibt die y-Werte des angepassten Modells aus, das den unabhängigen Werten in X entspricht.

  • i1ddbl.png Parameter für beste Anpassung —

    Parameter für beste Anpassung gibt das Array aus Parametern aus, mit denen der mittlere gewichtete Fehler zwischen Beste nichtlineare Anpassung und beobachteten Y-Werten minimiert wird.

  • i2ddbl.png Kovarianz —

    Kovarianz ist die Matrix der Kovarianzen.

    Cjk ist die Kovarianz zwischen a[j] und a[k]. c[jj] ist die Varianz von a[j]. Dieses VI erzeugt die Kovarianz Cgemäß der folgenden Gleichung: C = (0,5D)^-1 , wobei D die Hessian der Funktion in Bezug auf ihre Parameter ist.

  • ierrcodeclst.png Fehler (Ausgang) —

    Fehler (Ausgang) enthält Angaben zum Fehler. Dieser Ausgang ist ein Standardausgang zur Fehlerausgabe.

  • idbl.png Restbetrag —

    Restbetrag gibt den mittleren gewichteten Fehler zwischen Beste nichtlineare Anpassung und beobachteten Y-Werten aus.

    • Dieses VI berechnet mithilfe der Levenberg-Marquardt-Methode die Parameter für beste Anpassung, mit denen der mittlere gewichtete Fehler zwischen beobachteten Y-Werten und Beste nichtlineare Anpassung minimiert wird. Das Kurvenmodell wird durch folgende Gleichung bestimmt:

    y[i] = f(x[i], a0, a1, a2, …)

    wobei a0, a1, a2, … die Parameter sind.

    Für die Levenberg-Marquardt-Methode wird y nicht für eine lineare Beziehung mit den Parametern benötigt.

    Die Hesse-Matrix wird häufig für numerische Optimierungen wie die Newton-Methode eingesetzt. Um die Schwäche der singulären Hesse-Matrix zu vermeiden, wird mit der Levenberg-Marquardt-Methode der Hesse-Matrix eine positive definite Diagonalmatrix hinzugefügt. Diese positive definite Diagonalmatrix ist der Hauptunterschied zwischen der Levenberg-Marquardt- und der Gauß-Newton-Methode. Weitere Informationen zur Levenberg-Marquardt-Methode finden Sie unter Numerische Optimierung im Hilfethema Literaturhinweise zur Mathematik.

    Das nichtlineare Levenberg-Marquardt-Verfahren funktioniert sowohl für lineare als auch für nichtlineare Kurven. Zur Anpassung an lineare Kurven ist das VI Allgemeine lineare Anpassung jedoch besser geeignet. Da die Richtigkeit der Ergebnisse beim Levenberg-Marquardt-Verfahren nicht immer garantiert werden kann, müssen Sie die Ergebnisse nachprüfen.

    Beispiele

    Die folgenden Beispieldateien sind in LabVIEW enthalten.

    • labview\examples\Mathematics\Fitting\Ellipse fit.vi
    • labview\examples\Mathematics\Fitting\Sum of 3 Gaussians with offset fit.vi
    • labview\examples\Mathematics\Fitting\Gaussian surface with offset fit.vi