Führt eine eindimensionale Interpolation mithilfe einer ausgewählten Methode basierend auf der durch X und Y definierten Zuordnungstabelle durch.


icon

Ein-/Ausgänge

  • ci32.png Methode —

    Methode gibt das Interpolationsverfahren an.

    0Nächstgelegen—Wählt den Y-Wert, der zu X gehört und dem aktuellen xi-Wert am nächsten ist. Der interpolierte Wert wird auf den nächsten Datenpunkt gesetzt.
    1Linear—Setzt die interpolierten Werte auf Punkte entlang der Strecke zwischen X und Y.
    2Spline—Gewährleistet, dass die erste und zweite Ableitung der kubischen Interpolationspolynome stetig sind – sogar an den Datenpunkten selbst.
    3Hermite (kubisch)—Gewährleistet, dass die erste Ableitung der kubischen Interpolationspolynome stetig ist, und setzt die Ableitung an den Endpunkten auf bestimmte Werte, um die ursprüngliche Form und Monotonie der Y-Werte beizubehalten.
    4Lagrange—Verwendet den baryzentrischen Lagrange-Interpolationsalgorithmus.
  • c1ddbl.png Y —

    Y ist das Array mit den Werten der abhängigen Variablen (durch Tabulatoren getrennt).

  • c1ddbl.png X —

    X ist das Array mit den Werten der unabhängigen Variablen (durch Tabulatoren getrennt).

    Die Länge von X muss der Länge von Y entsprechen.

  • c1ddbl.png xi —

    xi gibt das Array mit den Werten der unabhängigen Variablen an, bei denen die interpolierten Werte yi der abhängigen Variablen berechnet werden sollen.

  • cbool.png X ist monoton —

    X ist monoton gibt an, ob die Werte in X monoton mit dem Index ansteigen.

    Wenn X ist monoton TRUE ist, muss der Interpolationsalgorithmus weder die Werte in X sortieren noch die Werte in Y entsprechend neu anordnen. Wenn X ist monoton FALSE lautet, sortiert dieses VI die X-Eingangs-Arrays aufsteigend. Anschließend wird Y entsprechend sortiert.

  • ci32.png n Mal —

    n Mal bestimmt die Interpolation von xi Stellen und gibt zwischen jedem Element Y interpolierte Werte aus, wenn xi leer ist. Die Interpolation zwischen Y Elementen wird n Mal wiederholt. Wenn an xi ein Wert anliegt, wird n Mal ignoriert.

  • i1ddbl.png yi —

    yi ist das Ausgangs-Array aus interpolierter Werte entsprechend der von xi unabhängigen Variablenwerte.

  • i1ddbl.png xi verwendet —

    xi verwendet ist ein 1D-Array aus Werten der ersten unabhängigen Variable, bei der interpolierte Werte der abhängigen Variable yi zu berechnen sind.

    Wenn xi leer ist, gibt xi verwendet (2n Mal – 1)*(N – 1) + N Punkte mit (2n Mal – 1) Punkten zwischen benachbarten Elementen in X aus, wobei N die Länge von X ist. Wenn Sie den Eingang xi verbinden, ignoriert dieses VI n Mal und xi verwendet entspricht xi.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Das VI arbeitet mit abhängigen und unabhängigen Variablen in Tabellenform (X und Y) und gibt die interpolierten Werte yi entsprechend jeder xi-Position aus. Das VI sucht in X nach jedem Wert von xi und ermittelt anschließend anhand der relativen Position in X den interpolierten Wert yi an der gleichen relativen Position in Y.

    Für das VI "1D interpolieren" gibt es fünf Interpolationsverfahren. In den folgenden Abschnitten werden die einzelnen Methoden näher erläutert. Gehen Sie beim Lesen der Abschnitte von folgender Situation aus:

    • X und Y liegen bereits in aufsteigender Reihenfolge vor.
    • xj und yj sind die Elemente von X und Y.
    • xim ist das m-te Element in xi und yim ist der entsprechende m-te abhängige Wert yi.

    Methode des naheliegendsten Werts

    Bei der Methode des naheliegendsten Werts wird nach dem Wert gesucht, der xi in X am nächsten liegt. Dann wird der dazugehörige y-Wert in Y yi zugeordnet, siehe folgender Graph.

    Lineare Methode

    Mit der linearen Methode wird yi an dem Linienabschnitt interpoliert, der die beiden Werte (xj, xj + 1) verbindet, wenn sich xi zwischen den Werten (xj, xj + 1) in X befindet, siehe folgender Graph.

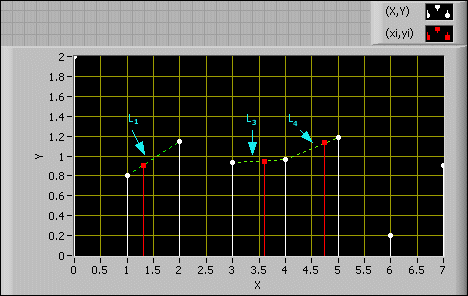
    Im vorigen Graph gilt folgende Gleichung als wahr:

    Spline-Methode

    Die Spline-Methode bezieht sich auf die kubische Spline-Methode. Bei dieser Methode bestimmt das VI für jedes Intervall zwischen zwei benachbarten Werten ein Polynom dritter Ordnung. Die Polynome erfüllen folgende Bedingungen:

    • Die ersten und zweiten Ableitungen bei xj sind stetig.
    • Die Polynome umfassen alle angegebenen Werte.
    • Die zweiten Ableitungen am Anfang und Ende betragen null.

    Der folgende Graph illustriert die kubische Spline-Methode.

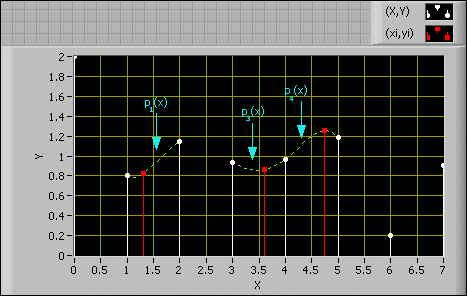
    Im vorigen Graphen ist Pj(x) das Polynom dritter Ordnung zwischen den beiden benachbarten Werten (xj, yj) und (xj + 1, yj + 1).

    Weitere Informationen zur kubischen Spline-Methode finden Sie unter A Practical Guide to Splines im Hilfethema Literaturhinweise zur Mathematik.

    Hinweis Wenn Sie die Spline-Methode wählen, liefert dieses VI die gleichen Ergebnisse wie das VI Spline-Interpolation 1D mit natürlichen Spline-Randbedingungen.

    Kubische Hermite-Methode

    Die kubische Hermite-Methode ist eine stückweise kubische Hermite-Interpolation. Bei dieser Methode wird für jedes Intervall ein Polynom dritter Ordnung in hermitescher Form ermittelt und sichergestellt, dass nur die ersten Ableitungen der Interpolationspolynome stetig sind. Im Vergleich zur kubischen Spline-Methode hat die kubische Hermite-Methode eine bessere lokale Eigenschaft. Wenn Sie also einen Wert xj ändern, liegt die Auswirkung auf das Interpolationsergebnis im Bereich zwischen [xj – 1, xj] und [xj, xj + 1].

    Weitere Informationen zur kubischen Hermite-Methode finden Sie unter A Practical Guide to Splines im Hilfethema Literaturhinweise zur Mathematik.

    Hinweis Wenn Sie die kubische Hermite-Methode wählen, liefert dieses VI die gleichen Ergebnisse wie das VI Hermite-Interpolation 1D .

    Lagrange-Methode

    The Lagrange method derives a polynomial of order N – 1 that passes all the N points specified in X and Y, where N is the length of X and Y. Diese Methode ist eine Abwandlung des Newton-Polynoms, bei der die Berechnung dividierter Differenzen vermieden wird. Die folgende Gleichung definiert die Lagrange-Methode:

    Wobei:

    Beachten Sie bei der Wahl einer Methode folgende Hinweise:

    • Die Methode des naheliegendsten Werts und die lineare Methode sind einfach anzuwenden, für die meisten Anwendungen aber zu ungenau.
    • Die Spline-Methode ergibt die glattesten Ergebnisse.
    • Die kubische Hermite-Methode hat eine bessere lokale Eigenschaft als die Spline- und die Lagrange-Methode.
    • Die Lagrange-Methode ist einfach zu implementieren, eignet sich aber nicht für untersuchende Berechnungen. Im Vergleich zur Spline-Methode ergibt die Lagrange-Methode ein Interpolationsergebnis mit extremen Ableitungen.

    Beispiele

    Die folgenden Beispieldateien sind in LabVIEW enthalten.

    • labview\examples\Mathematics\Interpolation\1D Interpolation.vi