Integriert die Werte von Array (Eingang) nach einem von vier gebräuchlichen Integrationsverfahren.

Zur Auswahl der polymorphen Instanz verbinden Sie Daten mit dem Eingang Array (Eingang) oder wählen Sie die Instanz manuell aus.


icon

Ein-/Ausgänge

  • c1ddbl.png Array (Eingang) —

    Array (Eingang) enthält die Werte für die Integralrechnung. Die Werte werden von einem Integranden f(t) bei Vielfachen von dt, also f(0), f(dt), f(2dt), … entnommen.

  • cdbl.png dt —

    dt ist die Intervallgröße. Dabei handelt es sich um die Argumentschrittweite, mit der die Werte für Array (Eingang) aus der Funktion ermittelt werden.

    Wenn Sie einen negativen Wert für dt angeben, verwendet das VI dessen Absolutwert.

  • ci32.png Integrationsverfahren —

    Integrationsverfahren ist das Verfahren, mit dem die Integralrechnung durchgeführt werden soll.

    0Trapez-Regel (Standard)
    1Simpson-Regel
    2Simpsonsche 3/8-Regel
    3Bode-Regel
  • idbl.png Ergebnis —

    Ergebnis ist das berechnete Integral.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Die x-Werte, die Sie an das VI anschließen, müssen in gleichmäßigem Abstand aufeinander folgen, sonst ist das Ergebnis falsch. Das Integral von Werten mit unregelmäßigen Abständen kann mit dem VI Numerische Integration (nicht äquidistant) berechnet werden.

    Numerische Integration (1D)

    WerteanzahlAnzahl der Rechenschritte
    22455 x Bode-Regel, 1 x Simpsonsche 3/8-Regel
    22556 x Bode-Regel
    22656 x Bode-Regel, Trapez-Regel
    22756 x Bode-Regel, 1 x Simpsonsche Regel
    22857 x Bode-Regel, 1 x Simpsonsche 3/8-Regel

    Wenn 224 Punkte vorliegen und nach der Bode-Regel vorgegangen wird, benötigt das VI 55 partielle Auswertungen nach der Bode-Regel und eine Auswertung nach der Simpsonschen 3/8-Regel, um zum Ergebnis zu gelangen.

    Alle Verfahren sind vom Auswertungsintervall (dt) abhängig. Das Integral wird bei diesen Verfahren mit Hilfe aufeinander folgender Anwendungen der Grundformel berechnet. Hierbei werden partielle Auswertungen durchgeführt, die von einer bestimmten Anzahl benachbarter Punkte abhängen. Die Anzahl der Punkte, die für jede partielle Berechnung verwendet werden, hängt von der Ordnung des Verfahrens ab. Das Ergebnis ist die Summe dieser aufeinander folgenden partiellen Auswertungen.

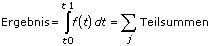
    wobei j ein Bereich ist, der von der Anzahl der Punkte und dem Integrationsverfahren abhängt.

    Die folgenden Grundformeln zur Berechnung der Partialsumme lauten folgendermaßen (die Verfahren sind in aufsteigender Ordnung angegeben):

    • Trapez-Regel: 1/2(x[i] + x[i + 1])*dt
    • Simpson-Regel: (x[2i] + 4x[2i + 1] + x[2i + 2])*dt/3, k = 2
    • Simpson-3/8-Regel: (3x[3i] + 9x[3i + 1] + 9x[3i + 2] + 3x[3i + 3]) * dt/8, k = 3

    • Bode: (14x[4i] +64x[4i + 1] +24x[4i + 2] +64x[4i + 3] +14x[4i + 4]) * dt/45, k = 4

      für i = 0, 1, 2, 3, 4, ..., Integralteil von [(N - 1)/k]

    wobei N die Anzahl der Punkte ist, k eine vom Verfahren abhängige natürliche Zahl und x das Eingangs-Array.

    Hinweis Wenn die Anzahl der Punkte, die für ein bestimmtes ausgewähltes Verfahren verwendet wird, keine ganzzahlige Anzahl von Partialsummen enthält, wird das Verfahren auf alle möglichen Punkte angewandt. Für die restlichen Punkte wird das nächstmögliche Verfahren mit niedrigerer Ordnung verwendet. Wenn beispielsweise die Bode-Regel ausgewählt wird, zeigt das obige Beispiel, wie die Auswertungen dieses VIs für verschiedene Anzahlen von Punkten aussehen.