Berechnet anhand des Verfahrens der kleinsten Quadrate, des kleinsten absoluten Residuums und des Biquadrats die lineare Anpassung mit den Werten X und Y.


icon

Ein-/Ausgänge

  • c1ddbl.png Y —

    Y ist das Array mit den abhängigen Werten. Die Länge von Y muss größer oder gleich der Anzahl unbekannter Parameter sein.

  • c1ddbl.png X —

    X ist das Array mit den unabhängigen Werten. X muss genauso groß sein wie Y.

  • c1ddbl.png Gewichtung —

    Gewichtung ist ein Array mit den Gewichtungen für die Beobachtungswerte X und Y. Gewichtung muss die gleiche Größe wie Y haben. Die Gewichtung muss auch Elemente ungleich 0 enthalten. Bei Elementen kleiner als 0 wird mit dem Absolutwert gearbeitet.

    Wenn kein Wert mit Gewichtung verbunden wird, setzt das VI alle Elemente von Gewichtung auf 1.

  • cdbl.png Toleranz —

    Toleranz gibt an, wann die iterative Anpassung von Steigung und Achsenabschnitt beim Verfahren des kleinsten Restbetrags oder beim Biquadrat-Verfahren beendet werden soll. Wenn beim Verfahren des kleinsten absoluten Residuums die relative Differenz von Restbetrag in zwei aufeinanderfolgenden Durchläufen kleiner ist als Toleranz, gibt das VI den resultierenden Restbetrag aus. Wenn beim Biquadrat-Verfahren die relative Differenz von Steigung und Achsenabschnitt in zwei aufeinanderfolgenden Durchläufen die Toleranz unterschreitet, gibt das VI die resultierenden Parameter Steigung und Achsenabschnitt aus.

    Bei einer Toleranz von kleiner oder gleich 0 wird die Toleranz auf 0,0001 gesetzt.

  • cu16.png Methode —

    Methode legt das Anpassungsverfahren fest.

    0Kleinste Quadrate (Standard)
    1Kleinstes absolutes Residuum
    2Biquadrat
  • cnclst.png Parametergrenzen —

    Parametergrenzen enthält die oberen und unteren Grenzwerte für Steigung und Achsenabschnitt. Wenn Ihnen die genauen Werte bestimmter Parameter bekannt sind, können Sie diese als Grenzwerte für die Parameter angeben.

  • cdbl.png Min. Anstieg —

    Min. Anstieg gibt die Untergrenze für Anstieg an. Die Standardeinstellung lautet -Inf, es gibt also keine untere Begrenzung für Steigung.

  • cdbl.png Max. Anstieg —

    Max. Anstieg gibt die Obergrenze für Steigung an. Die Standardeinstellung lautet Inf, es gibt also keine obere Begrenzung für Steigung.

  • cdbl.png Min. Achsenabschnitt —

    Min. Achsenabschnitt gibt die Untergrenze für Achsenabschnitt an. Die Standardeinstellung lautet -Inf, es gibt also keine untere Begrenzung für Achsenabschnitt.

  • cdbl.png Max. Achsenabschnitt —

    Max. Achsenabschnitt gibt die Obergrenze für Achsenabschnitt an. Die Standardeinstellung lautet Inf, es gibt also keine obere Begrenzung für Achsenabschnitt.

  • i1ddbl.png Beste lineare Anpassung —

    Beste lineare Anpassung gibt die y-Werte des angepassten Modells aus.

  • idbl.png Steigung —

    Steigung gibt die Steigung des angepassten Modells aus.

  • idbl.png Achsenabschnitt —

    Achsenabschnitt gibt den y-Achsenabschnitt des angepassten Modells aus.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

  • idbl.png Restbetrag —

    Restbetrag gibt den gewichteten mittleren Fehler des angepassten Modells aus. Wenn als Methode Kleinstes absolutes Residuum ausgewählt ist, handelt es sich bei Rest um den Betrag des Fehlers beim gewogenen Mittel. Ansonsten ist Rest kein Absolutwert.

    • Dieses VI nähert anhand des iterativen allgemeinen Verfahrens der kleinsten Quadrate und der Levenberg-Marquardt-Methode Versuchswerte an eine gerade Linie der allgemeinen Form nach folgender Gleichung an:

    f = ax + b

    wobei x die Folge von Eingangswerten X, a die Steigung und b der Achsenabschnitt ist. Mit diesem VI werden Werte für a und b ermittelt, die die Beobachtungswerte (X, Y) am besten darstellen.

    Die folgende Gleichung beschreibt die lineare Kurve, die der Algorithmus zur linearen Anpassung ergibt:

    y[i] = ax[i] + b

    Wenn das Rauschen in Y gaußverteilt ist, muss das Verfahren der kleinsten Quadrate angewandt werden. In der Abbildung ist die Linearanpassung dargestellt, die aus diesem Verfahren hervorgeht.

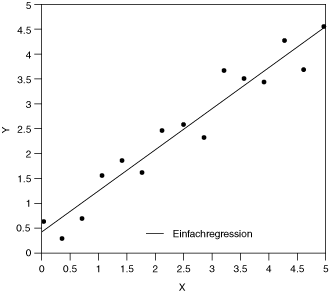
    Beim Verfahren der kleinsten Quadrate ermittelt das VI Steigung und Achsenabschnitt des linearen Modells durch Minimieren von Residuum nach folgender Gleichung:

    wobei N die Länge von Y, wi das i-te Element von Gewichtung, fi das i-te Element von Beste lineare Anpassung und yi das i-te Element von Y ist.

    Das Verfahren des kleinsten absoluten Residuums und das Biquadrat-Verfahren sind leistungsfähige Anpassungsverfahren. Sie sollten dann angewandt werden, wenn es unter den Beobachtungswerten Ausreißer gibt. In der Abbildung werden die Ergebnisse der Verfahren "Kleinstes Quadrat", "Kleinstes absolutes Residuum" und "Biquadrat" einander gegenübergestellt. In den meisten Fällen ist das Biquadrat-Verfahren weniger für Ausreißer empfänglich als das Verfahren des kleinsten absoluten Residuums.

    Beim Verfahren des Kleinsten absoluten Residuums ermittelt das VI Steigung und Achsenabschnitt des linearen Modells durch Minimieren von Residuum nach folgender Gleichung:

    Beim Biquadrat-Verfahren werden Steigung und Achsenabschnitt durch ein sich wiederholendes Verfahren ermittelt (vgl. folgende Abbildung) und der Restbetrag wird auf die gleiche Weise berechnet wie beim Verfahren der kleinsten Quadrate.

    Beispiele

    Die folgenden Beispieldateien sind in LabVIEW enthalten.

    • labview\examples\Mathematics\Fitting\Regression Solver.vi
    • labview\examples\Mathematics\Fitting\Linear, Exp, and Power Fit.vi
    • labview\examples\Mathematics\Fitting\Robust linear fit.vi