3D-ANOVA
- Aktualisiert2025-07-30
- 10 Minute(n) Lesezeit
Führt an einem Array mit Versuchsbeobachtungen, die auf verschiedenen Levels von zwei Faktoren gemacht wurden, eine Zweiwege-Varianzanalyse durch.

Ein-/Ausgänge
 Level
—
Level
—
Level ist ein Cluster mit drei Werten, die sowohl der Anzahl der Level der Faktoren A, B und C als auch den Auswirkungen der Faktoren A, B und C (des festen Ereignisses oder des Zufallsereignisses) entsprechen.
 X
—
X
—
X enthält alle Beobachtungsdaten.  Index A
—
Index A
—
Index A enthält den Level von Faktor A, zu dem die entsprechende Beobachtung gehört.  Index B
—
Index B
—
Index B enthält den Level von Faktor B, zu dem die entsprechende Beobachtung gehört.  Index C
—
Index C
—
Index C enthält den Level von Faktor C, zu dem die entsprechende Beobachtung gehört.  Beobachtungen pro Zelle
—
Beobachtungen pro Zelle
—
Beobachtungen pro Zelle ist die Anzahl der Beobachtungen in jeder Zelle. Diese ist für alle Zellen identisch.  Info
—
Info
—
Info ist eine (8, 4)-Matrix, die wie folgt strukturiert ist: Die erste Spalte entspricht der Summe der Quadrate, die den jeweiligen Faktoren (A, B, C), den jeweiligen Interaktionen (AB, AC, BC, ABC) und dem Restfehler zugeordnet sind. Die zweite Spalte entspricht den jeweiligen Freiheitsgraden. Die dritte Spalte entspricht den jeweiligen quadratischen Mittelwerten. Die vierte Spalte entspricht den jeweiligen F-Werten.   Signifikanz
—
Signifikanz
—
Signifikanz ist ein Cluster mit sieben numerischen Werten, die den Signifikanzniveaus entsprechen.
 Fehler
—
Fehler
—
Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode. |
Bei allen ANOVA-VIs wird nach Beweisen gesucht, dass die Faktoren oder Interaktionen zwischen den Faktoren eine maßgebliche Auswirkung auf die Versuchsergebnisse haben. Bei jedem Modell wird dazu eine andere Methode verwendet.
Zufällige und feste Effekte
Ein Faktor ist ein Zufallseffekt, wenn eine große Grundgesamtheit von Levels vorhanden ist, aber nicht aus allen Levels eine Stichprobe entnommen werden kann. Daher erheben Sie zufällige Stichproben und hoffen, eine Verallgemeinerung für alle Levels erzielen zu können. Ein Faktor ist ein fester Effekt, wenn Sie aus allen Levels eine Stichprobe entnehmen können.
Statistisches Modell
Die Gleichung xpqrs sei die s-te Beobachtung des p-ten, q-ten und r-ten Levels von A, B bzw. C, wobei s = 0, 1, ..., L – 1 ist. Jede Beobachtung wird als Summe von acht Komponenten ausgedrückt. Folglich gilt:
xpqrs = µ + αp + βq + γr + (αβ)pq + (αγ)pr + (βγ)qr + (αβγ)pqr + εpqrswobei
- µ der Gesamtmittelwert ist.
- αp ist die durchschnittliche Auswirkung derp-ten Stufe von Faktor A.
- βq ist die durchschnittliche Auswirkung derq-ten Stufe von Faktor B.
- γr ist die durchschnittliche Auswirkung derr-ten Stufe des Faktors C.
- (αβ)pq ist die zweifaktorielle Interaktion derp-ten Stufe von Faktor A mit derq-ten Stufe von Faktor B.
- (αγ)pr ist die zweifaktorielle Interaktion derp-ten Stufe von Faktor A mit derr-ten Stufe von Faktor C.
- (βγ)qr ist die zweifaktorielle Interaktion derq-ten Stufe von Faktor B mit derr-ten Stufe von Faktor C.
- (αβγ)pqr ist die dreifache Interaktion derp-ten Stufe von Faktor A, derq-ten Stufe von Faktor B und derr-ten Stufe von Faktor C.
- εpqrs ist eine zufällige Fluktuation.
Hypothesen
Jede der folgenden Hypothesen sagt auf andere Weise aus, dass ein Faktor oder eine Interaktion zwischen Faktoren keine Auswirkung auf experimentelle Ergebnisse hat. Bei diesem VI wird angenommen, dass es keine Auswirkungen gibt. Es werden dann Beweise gesucht, um diese Annahmen zu widerlegen. Die sieben Hypothesen sind die folgenden:
- (A), dass αp = 0 für alle Niveaus p , wenn Faktor A fest ist, und dassσA²= 0, wenn Faktor A zufällig ist.
- (B), dass βq = 0 für alle Niveaus q , wenn Faktor B fest ist, und dassσB²= 0, wenn Faktor B zufällig ist.
- (C) dass γr = 0 für alle Niveaus r , wenn der Faktor C fest ist, und dassσC²= 0, wenn der Faktor B zufällig ist.
- (AB), dass (αβ)pq = 0 für alle Niveaus p und q , wenn die Faktoren A und B fest sind, und dassσAB²= 0, wenn entweder Faktor A oder B zufällig ist.
- (AC) dass (αγ)pr = 0 für alle Niveaus p und q , wenn die Faktoren A und C fest sind, und dassσAC²= 0, wenn entweder Faktor A oder C zufällig ist.
- (BC) dass (βγ)qr = 0 für alle Niveaus p und q , wenn die Faktoren B und C fest sind, und dassσBC²= 0, wenn entweder Faktor B oder C zufällig ist.
- (ABC) dass (αβγ)pqr = 0 für alle Niveaus p, qund r , wenn die Faktoren A, B und C fest sind, und dassσABC²= 0, wenn einer der Faktoren A, B oder C zufällig ist.
Annahmen
Für das VI "3D ANOVA" gelten folgende Bedingungen:
- Nehmen wir an, dass für jedes p, qund r, εpqrs normalverteilt ist mit Mittelwert 0 und Varianzσe².
- Wenn ein Faktor A festgelegt ist, wird angenommen, dass die Grundgesamtheiten der Messungen auf jedem Niveau von A normalverteilt sind mit einem Mittelwert αp + µ und VarianzσA²normalverteilt sind und dass alle Populationen auf jedem Niveau die gleiche Varianz haben. Außerdem wird angenommen, dass αp gleich Null ist. Analoge Annahmen gelten für B und C.
- Wenn ein Faktor A zufällig ist, nehmen wir an, dass der Effekt des Niveaus von A selbst, αpeine normalverteilte Zufallsvariable mit Mittelwert 0 und VarianzσA²ist. Analoge Annahmen gelten für B und C.
- Wenn einige der Faktoren, wie z. B. A und B, die mit der Wirkung einer Interaktion verbunden sind, (αβ)pq fixiert sind, dann nehmen wir an, dass die Populationen der Messungen auf jedem Niveau von A und B normalverteilt sind mit Mittelwert µ + αp + βq + (αβ)pq und VarianzσAB². Für jedes feste psind die Mittel (αβ)pq bei der Summierung über alle qgleich Null. Analog dazu gilt für jedes feste q, dass (αβ)pq bei der Summierung über alle pgleich Null.
- Wenn einer der Faktoren, z. B. A und B, mit der Wirkung einer Wechselwirkung (αβ) verbunden istpq zufällig sind, wird angenommen, dass der Effekt eine normalverteilte Zufallsvariable mit Mittelwert 0 und VarianzσAB²ist. Wenn A fest, B aber zufällig ist, nehmen wir an, dass für jedes feste qdie Mittelwerte (αβ)pq bei der Summierung über alle pgleich Null sind. Wenn B fest, A aber zufällig ist, ist anzunehmen, dass für jedes feste p die Mittelwerte (αβ)pq bei der Summierung über alle qgleich Null sind.
- Es wird angenommen, dass alle Auswirkungen, die als Zufallsvariable angesehen werden, paarweise unabhängig sind.
Allgemeine Vorgehensweise
Bei sämtlichen Ereignissen wird die Gesamtsumme der Quadrate, tss, einem Maß für die Gesamtabweichung der Daten vom Gesamtmittelwert der Grundgesamtheit, in Teilsummen von Quadraten zerlegt.
tss = ssa + ssb + ssc + ssab + ssac + ssbc + ssabc + sseJede Teilsumme der Summe tss entspricht einem Maß für eine Abweichung, die auf einen bestimmten Faktor oder eine bestimmte Interaktion zwischen den Faktoren zurückgeht. Hier ist ssa ein Maß für die Abweichung aufgrund von Faktor A, ssb ein Maß für die Abweichung aufgrund von Faktor B, ssc ein Maß für die Abweichung aufgrund von Faktor c, ssab ein Maß für die Abweichung aufgrund der Interaktion zwischen Faktor A und B und so weiter für ssac, ssbc und ssabc. Des Weiteren ist sse ein Maß für die Abweichung aufgrund zufälliger Abweichung. Das VI dividiert die entsprechenden Werte durch die zugehörigen Freiheitsgrade, um die jeweiligen Durchschnittswerte msa, msb, msc, msab, msac, msbc, msabc und mse zu bestimmen. Wenn beispielsweise Faktor A eine starke Auswirkung auf die experimentellen Beobachtungen hat, ist msa relativ groß.
Prüfen der Hypothese
Für jede Hypothese berechnet das VI eine Zahl f, die verwendet wird, um die zugehörige Wahrscheinlichkeit sig zu bestimmen. Beispielsweise wird die Hypothese (A), nach der p für alle Level p gleich 0 ist (A entspricht festem Ereignis), nach folgender Gleichung berechnet:
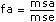
dann
sigA = Wahrscheinlichkeit{Fa – 1, abc(L – 1) > fa}wobei
Fa – 1, abc(L – 1)eine F-Verteilung mit den Freiheitsgraden a – 1 und abc(L – 1) ist. Sie können dann die Wahrscheinlichkeiten sigA, sigB, sigC, sigAB, …, sig ABC verwenden, um zu bestimmen, wann Sie die zugehörigen Hypothesen (A), (B), (C), (AB), ..., (ABC) verwerfen sollten.
Woran erkennen Sie, dass die Nullhypothese verworfen werden muss? Wählen Sie für jede Hypothese ein Signifikanzniveau aus. Damit wird die Wahrscheinlichkeit festgelegt, dass Sie die Hypothese fälschlicherweise verwerfen (im Allgemeinen wird der Wert 0,05 ausgewählt). Vergleichen Sie das ausgewählte Signifikanzniveau mit der ausgegebenen zugehörigen Wahrscheinlichkeit sig. Wenn die Wahrscheinlichkeit sig kleiner als das Signifikanzniveau ist, sollten Sie die Nullhypothese verwerfen. Wenn A beispielsweise ein zufälliger Effekt ist, das Signifikanzniveau 0,05 beträgt und sigA = 0,03 ist, müssen Sie die HypotheseσA²= 0 zurückweisen und zu dem Schluss kommen, dass der Faktor A einen Einfluss auf die experimentellen Beobachtungen hat.
Bei einigen Modellen gibt es für manche Hypothesen keine Möglichkeit der Überprüfung. In dem Fall lauten die Ausgangsparameter, die unmittelbar mit der Prüfung dieser Hypothesen in Verbindung stehen, –1,0.
Formeln
Es sei xpqrs die s-te Beobachtung des p-ten, q-ten und r-ten Levels von A, B bzw. C, wobei s = 0, 1, ..., L – 1 ist.
Es sei
a = |A Level|
b = |B Level|
c = |C Level|
dann




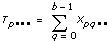







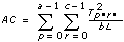
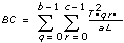

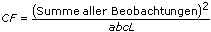





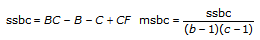

 Sig A
—
Sig A
—