2D-ANOVA
- Aktualisiert2025-07-30
- 11 Minute(n) Lesezeit
Es wird ein Array mit experimentellen Beobachtungen verwendet, die auf verschiedenen Leveln von zwei Faktoren gemacht wurden, und eine Zweiwege-Varianzanalyse durchgeführt.

Ein-/Ausgänge
 A-Level
—
A-Level
—
A-Level enthält die Anzahl der Level von Faktor A. Das Vorzeichen von A-Level ist positiv, wenn A unveränderlich ist, und negativ, wenn A eine Zufallsgröße ist  X
—
X
—
X enthält alle Beobachtungsdaten.  Index A
—
Index A
—
Index A enthält den Level von Faktor A, zu dem die entsprechende Beobachtung gehört.  Index B
—
Index B
—
Index B enthält den Level von Faktor B, zu dem die entsprechende Beobachtung gehört.  Beobachtungen pro Zelle
—
Beobachtungen pro Zelle
—
Beobachtungen pro Zelle ist die Anzahl der Beobachtungen in jeder Zelle. Diese ist für alle Zellen identisch.  B-Level
—
B-Level
—
B-Level enthält die Anzahl der Level von Faktor B. Das Vorzeichen von B-Level ist positiv, wenn B unveränderlich ist, und negativ, wenn B eine Zufallsgröße ist.  Info
—
Info
—
Info ist eine (4, 4)-Matrix, die wie folgt aufgebaut ist: Die erste Spalte entspricht der Summe der Quadrate, die dem Faktor A, Faktor B, der Interaktion von AB und dem Restfehler zugeordnet ist. Die zweite Spalte entspricht den jeweiligen Freiheitsgraden. Die dritte Spalte entspricht den jeweiligen quadratischen Mittelwerten. Die vierte Spalte entspricht den jeweiligen F-Werten.   Sig A
—
Sig A
—
sig A ist das berechnete Signifikanzniveau, das Faktor A zugeordnet ist.  Sig B
—
Sig B
—
sig B ist das berechnete Signifikanzniveau, das Faktor B zugeordnet ist.  Sig AB
—
Sig AB
—
sig AB ist das berechnete Signifikanzniveau, das der Interaktion der Faktoren A und B zugeordnet ist.  Fehler
—
Fehler
—
Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode. |
Faktoren, Level und Zellen
Ein Faktor bildet die Grundlage für die Kategorisierung von Werten. Wenn Sie beispielsweise zählen möchten, wie häufig Probanden ihren Oberkörper aus der Rücklage aufrichten können, ist das Alter eine Grundlage für die Kategorisierung. Für das Alter könnten folgende Level gelten:
| Level 0 | 6 bis 10 Jahre alt |
| Level 1 | 11 bis 15 Jahre alt |
Ein weiterer möglicher Faktor stellt das Gewicht mit folgenden Größen dar:
| Level 0 | unter 50 kg |
| Level 1 | zwischen 50 und 75 kg |
| Level 2 | über 75 kg |
Angenommen, Sie haben eine Reihe von Beobachtungen an n Personen durchgeführt und das Ergebnis sieht wie folgt aus:
| Proband 1 | 8 Jahre alt (Level 0) | 30 kg (Level 0) | 10 Mal |
| Proband 2 | 12 Jahre alt (Level 1) | 40 kg (Level 0) | 15 Mal |
| Proband 3 | 15 Jahre alt (Level 1) | 76 kg (Level 2) | 20 Mal |
| Proband 4 | 14 Jahre alt (Level 1) | 60 kg (Level 1) | 25 Mal |
| Proband 5 | 9 Jahre alt (Level 0) | 51 kg (Level 1) | 17 Mal |
| Proband 6 | 10 Jahre alt (Level 0) | 80 kg (Level 2) | 4 Übungen |
und so weiter.
Wenn Sie Beobachtungen als Funktion von Faktor A und Faktor B darstellen, gehören sie zu den Zellen einer Matrix, in der Faktor A den Zeilen und Faktor B den Spalten entspricht. Jede Zelle muss mindestens eine Beobachtung enthalten. Des Weiteren muss jede Zelle dieselbe Anzahl von Beobachtungen enthalten.
Sie stellen dazu die Beobachtungen in Form eines Arrays X mit den Werten 10, 15, 20, 25, 17 und 4 bereit. Mit Hilfe des Arrays Index A wird der Level (die Kategorie) festgelegt, für den die Beobachtung gilt. Im vorliegenden Fall enthält das Array die Werte 0, 1, 1, 1, 0 und 0.
Mit Hilfe des Arrays Index B wird der Level von Faktor B festgelegt, für den die Beobachtung gilt. Im vorliegenden Fall enthält das Array die Werte 0, 0, 2, 1, 1 und 2. Schließlich gibt es zwei mögliche Level für Faktor A und drei mögliche Level für Faktor B. Daher geben Sie als A-Level 2 und als B-Level 3 ein.
Sie können eines der folgenden Modelle anwenden, wobei L den Beobachtungen pro Zelle entspricht:
- Modell 1: Fixed-Effects-Modell ohne Interaktion und einer Beobachtung pro Zelle (pro vorgegebenem Level x und y des Faktors A bzw. B).
- Modell 2: Fixed-Effects-Modell mit Interaktion und L > 1 Beobachtungen pro Zelle.
- Modell 3: Beide Fixed-Effects-Modelle mit Interaktion und L > 1 Beobachtungen pro Zelle.
- Modell 4: Random-Effects-Modell mit Interaktion und L > 1 Beobachtungen pro Zelle.
Feste und zufällige Effekte
Ein Faktor ist ein Zufallseffekt, wenn eine große Grundgesamtheit von Levels vorhanden ist, aber nicht aus allen Levels eine Stichprobe entnommen werden kann. Daher erheben Sie zufällige Stichproben und hoffen, eine Verallgemeinerung für alle Levels erzielen zu können. Ein Faktor ist ein fester Effekt, wenn Sie aus allen Levels eine Stichprobe entnehmen können.
Mit den Eingangsparametern A-Level und B-Level wird die Anzahl der Level von Faktor A bzw. B angegeben, und ob die Faktoren einem festen oder Zufallseffekt entsprechen. Wenn beispielsweise der Faktor A zufällig ist, setzen Sie die A-Stufen so, dass die Anzahl der Stufen in Faktor A negativ ist. Wenn es nur eine Beobachtung pro Zelle gibt, müssen sowohl die A- als auch die B-Werte positiv sein. Das bedeutet, dass Sie Modell 1 verwenden.
Statistisches Modell
Es sei die Gleichung xpqr die r-te Beobachtung des p-ten und q-ten Levels von A bzw. B, wobei r = 0, 1, ..., L – 1 ist.
Bei Modell 1 wird jede Beobachtung als Summe von vier Komponenten ausgedrückt.
xpqr = µ + αp + βq + εpqrBei Modell 2, 3 und 4 wird jede Beobachtung als Summe von fünf Komponenten ausgedrückt.
xpqr = µ + αp + βq + (αβ)pq + εpqrwobei
βq = µq - µ- µ ist die mittlere Gesamtwirkung (der Durchschnitt der mittleren Wirkung für alle Grundgesamtheiten).
- αp ist die Auswirkung derp-ten Stufe von Faktor A (gleich µp - µ, wobei µp der Durchschnitt derp-ten Stufe von Faktor A über alle Stufen von Faktor B ist).
- βq ist die Auswirkung derq-ten Stufe von Faktor B (gleich µq - µ, wobei µq der Durchschnitt derq-ten Stufe von Faktor B über alle Stufen von Faktor A ist).
- (αβ)pq ist die Wechselwirkung zwischen derp-ten Stufe von Faktor A und derq-ten Stufe von Faktor B (gleich µpq - (µ + αp + βq), wobei µpq der Populationsmittelwert derpq-ten Zelle ist).
- εpqr ist die Abweichung von xpqr vom Mittelwert der Antwort für diepq-te Population.
Hypothesen
Jede der folgenden Hypothesen sagt auf andere Weise aus, dass ein Faktor oder eine Interaktion zwischen Faktoren keine Auswirkung auf experimentelle Ergebnisse hat. Bei diesem VI wird angenommen, dass es keine Auswirkungen gibt. Es werden dann Beweise gesucht, um diese Annahme zu widerlegen. Im Folgenden die drei Hypothesen:
- (A), dass αp = 0 für alle Niveaus p , wenn Faktor A fest ist, und dassσA²= 0, wenn Faktor A zufällig ist.
- (B), dass βq = 0 für alle Niveaus q , wenn Faktor B fest ist, und dassσB²= 0, wenn Faktor B zufällig ist.
- (AB), dass (αβ)pq = 0 für alle Niveaus p und q , wenn die Faktoren A und B fest sind, und dassσA²= 0, wenn entweder Faktor A oder Faktor B zufällig ist. (Dies gilt nicht für Modell 1. Bei Modell 1 gibt es keine Interaktion und die zugehörigen Ausgangsparameter sind überflüssig.)
Annahmen
Das VI "2D ANOVA" funktioniert nur unter folgenden Bedingungen:
- Nehmen wir an, dass für jedes p, qund r, εpqr normalverteilt ist mit Mittelwert 0 und Varianzσe².
- Wenn ein Faktor wie A fest ist, wird angenommen, dass die Grundgesamtheiten der Messungen auf jedem Niveau von A normalverteilt sind mit Mittelwert αp + µ und VarianzσA²normalverteilt sind und dass alle Populationen auf jedem Niveau die gleiche Varianz haben. Außerdem wird angenommen, dass αp gleich Null ist. Analoge Annahmen gelten für B.
- Ist ein Faktor wie A zufällig, so ist davon auszugehen, dass die Wirkung der Höhe von A selbst, αpeine normalverteilte Zufallsvariable mit Mittelwert 0 und Varianzσe²ist. Analoge Annahmen gelten für B.
- Wenn alle Faktoren wie A und B, die mit dem Effekt einer Wechselwirkung (αβ)pq fixiert sind, nehmen wir an, dass die Grundgesamtheiten der Messungen auf jeder Ebene normalverteilt sind mit dem Mittelwert µpq und VarianzσAB². Für jedes feste p, (αβ)pq gleich Null, wenn man über alle qsummiert. In ähnlicher Weise sind für jedes feste qdie Mittelwerte (αβ)pq gleich Null, wenn man über alle psummiert.
- Wenn einer der Faktoren wie A und B, die mit der Wirkung einer Wechselwirkung (αβ)pq zufällig sind, wird angenommen, dass der Effekt eine normalverteilte Zufallsvariable mit Mittelwert 0 und VarianzσAB²ist. Wenn A fest, B aber zufällig ist, dann wird auch angenommen, dass für jedes feste q die MittelwerteσAB²bei der Summierung über alle pgleich Null sind. Ähnlich verhält es sich, wenn B fest, A aber zufällig ist: Für jedes feste p summieren sich die MittelwerteσAB²über alle qzu Null.
- Außerdem wird davon ausgegangen, dass alle Auswirkungen, die als Zufallsvariable angesehen werden, paarweise unabhängig sind.
Allgemeine Vorgehensweise
Bei sämtlichen Modellen wird die Gesamtsumme tss der Quadrate, einem Maß für die Gesamtabweichung der Daten vom Gesamtmittelwert der Grundgesamtheit, in Teilsummen von Quadraten zerlegt. Bei Modell 1
tss = ssa + ssb + sseBei Modell 2 bis 4 hingegen lautet sie:
tss = ssa + ssb + ssab + sseJede Teilsumme von tss entspricht einem Maß für eine Abweichung, die auf einen bestimmten Faktor oder eine bestimmte Interaktion zwischen den Faktoren zurückgeht. Hier ist ssa ein Maß für die Abweichung aufgrund von Faktor A, ssb ein Maß für die Abweichung aufgrund von Faktor B, ssab ein Maß für die Abweichung aufgrund der Interaktion zwischen Faktor A und B und sse ein Maß für die Abweichung aufgrund zufälliger Abweichung. Beachten Sie, dass der Term ssab bei Modell 1 nicht vorhanden ist. Das bedeutet, es ist keine Interaktion vorhanden.
Das VI dividiert die Werte ssa, ssb, ssab und sse durch deren jeweilige Freiheitsgrade, um die mittleren quadratischen Größen msa, msb, msab und mse zu berechnen. Wenn sich ein Faktor, also etwa Faktor A, stark auf die experimentellen Beobachtungen auswirkt, ist die entsprechende mittlere quadratische Größe msa relativ groß.
Prüfen der Hypothese
Für jede Hypothese berechnet das VI eine Zahl f, die ihrerseits verwendet wird, um die Wahrscheinlichkeit sig zu bestimmen. Zum Beispiel für die Hypothese (A), dass αp = 0 für alle Niveaus p, (festes A), berechnet das VI
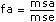
dann
sigA = Wahrscheinlichkeit{Fa – 1, (a – 1)(b – 1)} > fawobei
Fa – 1, (a – 1)(b – 1)eine F-Verteilung mit den Freiheitsgraden a – 1 und (a – 1)(b – 1) ist. Nun können Sie anhand der Wahrscheinlichkeiten sigA, sigB und sigAB bestimmen, wann die zugehörigen Hypothesen (A), (B) und (AB) verworfen werden sollten.
Woran erkennen Sie, dass die Nullhypothese verworfen werden muss? Wählen Sie für jede Hypothese ein Signifikanzniveau aus. Damit wird die Wahrscheinlichkeit festgelegt, dass Sie die Hypothese fälschlicherweise verwerfen (im Allgemeinen wird der Wert 0,05 ausgewählt). Vergleichen Sie das ausgewählte Signifikanzniveau mit der ausgegebenen zugehörigen Wahrscheinlichkeit sig. Wenn die Wahrscheinlichkeit sig kleiner als das Signifikanzniveau ist, sollten Sie die Nullhypothese verwerfen.
Wenn A beispielsweise ein zufälliger Effekt ist, das von Ihnen gewählte Signifikanzniveau 0,05 beträgt und das Ergebnis sigA 0,03 ist, müssen Sie die Hypothese αA² = 0 zurückweisen und zu dem Schluss kommen, dass der Faktor A einen Einfluss auf die experimentellen Beobachtungen hat.
Formeln
Es sei die Gleichung xpqr die r-te Beobachtung des p-ten und q-ten Levels von A bzw. B, wobei r = 0, 1, …, L – 1 ist.
Es sei
a = |A Level|
b = |B Level|








dann



dofab = (a – 1)(b – 1), wenn L > 1
dofab = 0, wenn L = 1

dofe = ab(L – 1), wenn L > 1
dofe = (a – 1)(b – 1), wenn L = 1





sigA =Wahrscheinlichkeit{Fa - 1, ab(L - 1) > fa}, wenn B fest ist
sigA =Prob{Fa - 1, (a - 1)(b - 1) > fa} wenn B zufällig ist
sigB =Wahrscheinlichkeit{Fa - 1, ab(L - 1) > fb}, wenn A fest ist
sigB =Prob{Fa - 1, (a - 1)(b - 1) > fb} wenn A zufällig ist
sigAB = Wahrscheinlichkeit{F(a – 1)(b – 1), ab(L – 1) > fab}