Berechnet das Kreuzleistungsspektrum Sxy der Eingangssignale X und Y. Zur Auswahl der polymorphen Instanz verbinden Sie Daten mit dem Eingang X oder wählen Sie die Instanz manuell aus.


icon

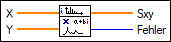
Ein-/Ausgänge

  • c1dcdb.png X —

    X ist die erste Folge komplexer Eingangswerte.

  • c1dcdb.png Y —

    Y ist die zweite Folge komplexer Eingangswerte.

  • i1dcdb.png Sxy —

    Sxy ist das Kreuzleistungsspektrum der Eingangssignale X und Y.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • Das Kreuzleistungsspektrum Sxy(f) der Signale x(t) und y(t) wird über folgende Gleichung bestimmt:

    Sxy(f) = X*(f)Y(f)

    wobei X*(f) die Komplex-Konjugierte von X(f) ist,

    X(f) =F{x(t)}, Y(f) =F{y(t)}.

    Bei diesem VI wird das Kreuzleistungsspektrum entweder mit der FFT oder DFT berechnet, die über die folgende Gleichung gegeben ist:

    ,

    wobei Sxy die komplexe Folge Sxy ist und n die Anzahl der Samples, die sowohl die Folge X als auch die Folge Y aufnehmen kann.

    Die maximale Kreuzleistung, die dieses VI mit der FFT ermitteln kann, ist 223 (8.388.608 oder 8M).

    Hinweis Einige Lehrbücher definieren das Kreuzleistungsspektrum als S'xy(f) = X(f)Y*(f). Wenn Sie lieber mit dieser Definition arbeiten, verwenden Sie die komplex Konjugierte der Ausgangsfolge Sxy. Das VI führt den Real- und den Imaginärteil separat aus. Für Ergebnisse für S'xy(f) kann jedoch das folgende Schema verwendet werden.

    Wenn die Anzahl der Samples in X und Y übereinstimmt und eine gültige Potenz von 2 ist,

    n = m = 2k

    für k = 1, 2, 3,…, 23,

    wobei n die Anzahl der Samples in X und m die Anzahl der Samples in Y ist, ruft das VI zur Berechnung der komplexen Kreuzleistungsfolge direkt die FFT-Routine auf. Dadurch wird eine schnelle Ausführung und effiziente Speicherleistung erzielt, da die Operationen jeweils sofort ausgeführt werden.

    Wenn die Anzahl der Samples in X und Y nicht übereinstimmt,

    n ≠ m

    wobei n die Anzahl der Samples in X und m die Anzahl der Samples in Y ist, gleicht das VI zunächst die Größe der kleineren Folge an, indem diese mit Nullen auffüllt. Ist diese Größe eine gültige Potenz von 2,

    Max(n,m) = 2k

    für k = 1, 2, 3,…, 23,

    wird zur Berechnung des Kreuzleistungsspektrums die FFT eingesetzt. Ansonsten wird die langsamere DFT verwendet. Demnach ist die Größe der komplexen Ausgangsfolge

    Größe = max(n,m)