Berechnet die Faltung der Eingangsfolgen X und Y. Zur Auswahl der polymorphen Instanz verbinden Sie Daten mit dem Eingang X oder Y oder wählen Sie die Instanz manuell aus.


icon

Ein-/Ausgänge

  • c1ddbl.png X —

    X ist die erste Eingangsfolge.

  • c1ddbl.png Y —

    Y ist die zweite Eingangsfolge.

  • cenum.png Algorithmus —

    Algorithmus gibt die zu verwendende Faltungsmethode an. Wenn Algorithmus auf direct eingestellt ist, wird die Faltung anhand des direkten Verfahrens der linearen Faltung berechnet. Bei frequency domain berechnet das VI die Faltung nach einem Verfahren, das auf der FFT beruht.

    Wenn X und Y klein sind, ist die Methode direct in der Regel schneller. Wenn X und Y groß sind, ist die Methode frequency domain in der Regel schneller. Daneben kann es zwischen den zwei Verfahren geringe Abweichungen geben.

    0
    direct
    1
    frequency domain
    (Voreinstellung)
  • i1ddbl.png X * Y —

    X * Y ist die Faltung von X und Y.

  • ii32.png Fehler —

    Fehler gibt alle Fehler oder Warnungen des VIs aus. Zur Umwandlung eines Fehlercodes oder einer Warnung in einen Fehler-Cluster verbinden Sie Fehler mit dem VI Fehler-Cluster aus Fehlercode.

    • 1D-Faltung

    Die lineare Faltung der Signale x(t) und y(t) ist folgendermaßen definiert:

    wobei das Symbol * für lineare Faltung steht.

    Wenn Algorithmus auf direkt eingestellt ist, wird die diskrete Implementierung der linearen Faltung zur Ermittlung von X * Y nach folgender Gleichung berechnet:

    für i = 0, 1, 2, … , M+N–2

    wobei h gleich X * Y,

    N ist die Anzahl der Elemente in X, M ist die Anzahl der Elemente in Y, die indizierten Elemente außerhalb der Bereiche von X und Y sind gleich Null, wie aus den folgenden Beziehungen hervorgeht:

    xj = 0, j < 0, oder j ≥ N

    und

    yj = 0, j < 0, oder j ≥ M.

    Wenn Algorithmus auf Frequenzbereich eingestellt ist, wird die lineare Faltung durch Befolgung der folgenden Schritte berechnet:

    • Zuerst wird das Ende von X und Y mit Nullen aufgefüllt, so dass beide die Länge M + N – 1 haben (vgl. die folgenden Gleichungen).
    • Als Zweites führt das VI anhand der folgenden Gleichungen die Fourier-Transformation von X' und Y' durch:
    X'(f) = FFT(x') Y'(f) = FFT(y')
    • Danach wird X'(f) mit Y'(f) multipliziert und die inverse Fourier-Transformation des Produkts gebildet. Das Ergebnis davon ist die lineare Faltung von X und Y, wie in der folgenden Gleichung dargestellt:
    X * Y = IFFT(X'(f) · Y'(f))

    Auf diese Weise wird eine lineare Faltung, keine zirkuläre erzielt. Da jedoch x(t) * y(t)N ⇔ X(f)Y(f) ein Fourier-Transformationspaar ist, wobei x(t) * y(t)N die zirkuläre Faltung von x(t) und y(t) ist, können Sie eine zirkuläre Version der Faltung erstellen. Zur Berechnung der zirkulären Faltung können Sie das Blockdiagramm zum Beispiel so aufbauen, wie in der folgenden Abbildung dargestellt.

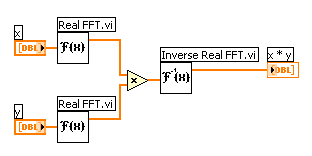
    Beispiele

    Die folgenden Beispieldateien sind in LabVIEW enthalten.

    • labview\examples\Signal Processing\Signal Operation\Edge Detection with 2D Convolution.vi