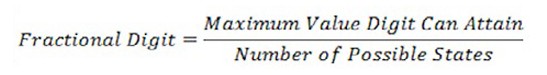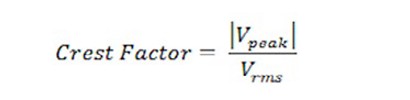数字万用表测量基础知识

实际上，每个DMM都具有直流和交流测量功能。电压测试通常用于测试和验证仪器、组件或电路的输出。电压总是在两点之间进行测量，因此需要两个探针。一些DMM连接器和探针是彩色的；红色用于测量正极点，黑色用于测量负极点，通常是一个参考点或接地点。然而，电压是双向的，所以如果正负极反接，测得的电压值就会变成相反数。

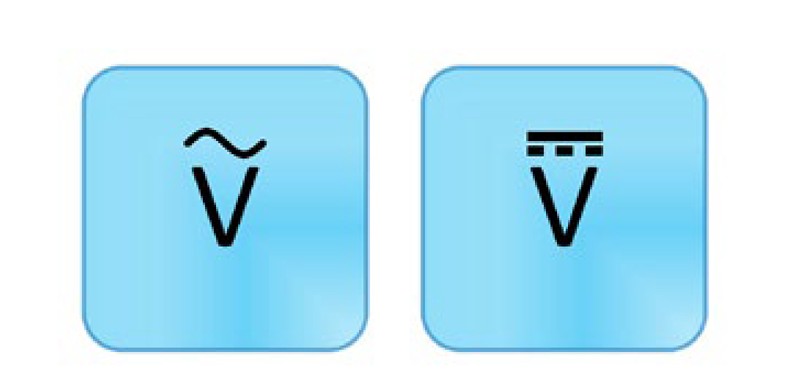
电压测量通常有两种不同的模式：直流和交流。通常，直流用一个V、一条虚线和一条实线表示；交流则用一个V和一条波浪线表示。务必确保为应用选择正确的量程和模式。

^{图1.交流电压（左）和直流电压（右）测量通常用于测试和验证仪器、组件或电路的输出。}

在测量交流或直流电压时，需要了解几个术语和概念。

输入电阻

理想电压表的输入电阻应无限大，这样仪器就不会消耗测试电路中的任何电流。但在实际测量中，总会有一些因素影响测量精度。为了尽可能减少这个问题，DMM的电压测量子系统的阻抗通常设计为几MΩ到几十MΩ。但如果测量的是低电压，即使是该范围内的阻值，测量也会存在不可接受的误差。因此，电压量程越低，选择的阻抗通常越高，如10 GΩ。

有些DMM可以选择输入电阻。对于大多数应用来说，阻抗越高，测量越准确。但是，有些情况下需要选择较低的阻抗。例如，如果导管内部存在多条不同导线，那么导线之间可能存在耦合。即使导线开路和浮地，DMM仍能够读取电压值。较高阻抗无法消除这些虚电压，但低阻抗可为这些累积的电荷提供一条路径，使得DMM能够正确测量出0 V。较低电压范围的一个范例是电路中线路之间靠得很近。

波峰因数

在测量交流信号（电压或电流）时，波峰因数是确定特定波形精度的重要参数。波峰因数是峰值与均方根值的比值，是一种描述波形形状的方法。通常，波峰因数用于电压测量，但也可用于电流测量等其他测量。从技术上说，波峰因数为正实数，但通常是一个比值。

^{公式2.波峰因数是衡量波形中峰值极端程度的指标}

对于没有峰值的恒定波形，由于波形的峰值与均方根值相等，因此波峰因数为1。对于三角波形，其波峰因数为1.732。波峰因数越高，波峰越尖锐，要获得准确的交流测量值也就越困难。

^{图2.交流信号的波峰因数会影响测量精度}

对于使用真均方根值进行测量的交流万用表，其精度基于正弦波测量值。它通过波峰因数来表明正弦波的失真程度，而且仍然可以在规定的精度范围内进行测量。它还包括其他波形的任何额外精度误差，具体取决于其波峰因数。

例如，如果给定DMM的交流精度为读数的0.03%。如果测量的是三角波形，需要查找波峰因数为1.732的任何额外误差。DMM规定，对于介于1和2之间的波峰因数，读数有0.05%的额外误差。因此，测量的精度为0.03% + 0.05%，总误差为读数的0.08%。可以看出，波形的波峰因数对测量精度影响非常大。

偏移量归零

大多数DMM具有偏移量归零的功能。该功能有助于消除直流电压或电阻测量时由于连接和导线引起的误差。首先，选择正确的测量类型和量程。然后将探针连接在一起，等待读取测量值。然后选择偏移量归零按钮。将得到的读数减去指零测量时的读数，就可以得到较为准确的读数。

自动归零

除了偏移量归零之外，另一种提高电压和电阻测量精度的方法是启用自动调零功能。自动调零用于补偿仪器内部的偏移。启用该功能后，每一次测量时DMM都会进行额外的测量。该测量是在DMM输入端和接地端之间进行的。然后从测量值中减去该值，即减去测量路径或ADC中的任何偏移量。虽然自动调零有助于提高测量精度，但会增加测量所需的时间。

另一个常见的测量功能是直流和交流电流测量。电压是通过与电路并联进行测量，而电流则是通过与电路串联来进行测量。这意味着需要断开电路（物理上中断电流的流动），以便将DMM插入电路回路中进行精确的测量。与电压类似，电流也是双向的。表示方法也非常类似，但符号用的是A而不是V。A代表安培，即电流的计量单位。务必确保为应用选择正确的量程和模式。

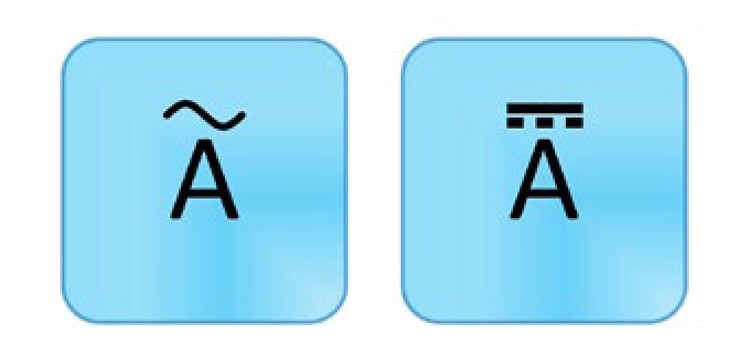
^{图3.直流电流（左）和交流电流（右）测量有助于对电路或组件进行故障分析。}

DMM在输入端存在小电阻，用于测量电压。然后根据欧姆定律可计算出电流。电流等于电压除以电阻。为了保护万用表，请勿在电流流过电路时断开电流测量功能。在电流测量模式下，还应避免意外测量电压，因为这可能导致保险丝熔断。如果保险丝不小心熔断，通常可以进行更换。有关详细信息，请参阅仪器说明书。

电阻测量通常用于测量电阻器或其他组件的电阻，如传感器或扬声器。电阻测量的工作原理是将一个已知的直流电压施加到内阻较小的未知串联电阻上。通过测量测试电压，即可计算出未知电阻的阻值。因此，只能在设备未通电时进行测试；否则，电路中已有的电压会导致读数不准确。还要记住，组件应在插入电路之前进行测量；否则，测量的是所有与组件连接的元件的电阻，而不仅仅是组件本身的电阻。

电阻的一个优点是无方向性，这意味着如果探针反接，读数仍然是相同的。电阻测量的符号为Ω，即电阻的计量单位。务必确保为应用选择正确的量程和模式。如果读数显示为OL，这意味着读数超出了上限或大于仪表在该量程内可以测量的值。正如之前提到的，使用偏移量归零可以提高测量值的准确性。

^{图4.电阻测量通常用于测量电阻器或其他组件的电阻。}

许多DMM还具有两个额外的测量功能：二极管测试和连续性测试。

连续性测试

连续性测试有助于确定两点之间何时存在电气连接。这可有助于进行断线处、印刷电路板(PCB)迹线或焊点故障分析。在测试连续性时，必须精准地找到探针接触的位置，以便进行监测。因此，大多数DMM在检测到闭合电路时会发出提示声，使您无需从探针处抬头查看。因此，连续性的符号看起来像一个声波。

^{图5.连续性测试有助于确定两点之间何时存在电气连接。}

连续性测试的工作原理与电阻测量一样；因此，在测试时，务必保证设备未通电。让测试探针的尖端触碰在一起，如果发出蜂鸣声，则表明连接正常，这非常有帮助。如果没有听到声音，那么请检查探针的连接是否牢固、DMM电池电量是否充足，以及所选的模式是否正确。此外还可查看用户手册，以确定发出声音需要的电阻量级，该参数因不同型号而异。

如果测试的电路存在大电容，则可能会听到一声快速的蜂鸣声，随后便静止。这是因为DMM施加到电路上的电压正在给电容器充电，在此期间，DMM认为这是一个闭合电路，但实际上并非如此。

二极管测试

二极管测试显示的是二极管的正向压降，单位为伏特。以下符号，毫无疑问就是二极管的符号。

^{图6.二极管测试显示的是二极管的正向压降，单位为伏特}

DMM促使小电流通过二极管，然后测量两条测试引线之间的压降。当测量二极管时，正极探针放置于阳极侧，负极探针放置于阴极侧。硅二极管的电压读数通常约为0.7 V，但电压范围只要在0.5到0.9 V之间，二极管仍旧可以正常运行。锗二极管的电压通常在0.3 V左右。

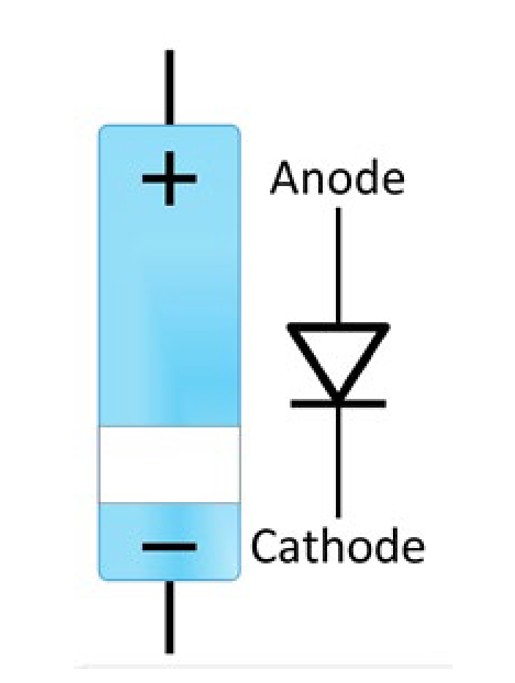
^{图7.通常，测试二极管时，正极探针放置于阳极侧，负极探针放置于阴极侧。但是将探针反接也能反映一些问题。}

接下来将正负探针反接，使负极探针在阳极一侧，正极探针在阴极一侧。如果二极管正常运行，万用表会显示OL，表示电路为开路。

如果二极管存在故障，可能是二极管短路或二极管开路。如果二极管故障导致开路，则无论是正向偏置还是反向偏置，DMM都将显示OL，因为流过的电流为零，相当于开路。如果二极管短路，DMM显示为0 V，因为二极管上没有压降。

在进行测量时，噪声是一个非常重要的考量因素。为了更好地理解仪器和测量中存在的相关噪声，需要熟悉另外两个参数。

常模抑制比(NMRR)描述了DMM对出现在两个输入端之间的噪声（即混合在测量信号中的噪声）的抑制能力。大多数噪声来自于线路频率及其谐波。NMRR通常用于表示仪器抑制50或60 Hz电源线噪声的能力，仅在指定频率下有效，在直流测量中非常实用。常模噪声也可以通过使用屏蔽或滤波来降低。

共模抑制比(CMRR)描述了DMM抑制两个输入端公共噪声的能力，如来自嘈杂环境的噪声。共模噪声通常比常模噪声要轻。

NMRR和CMRR通常在50 Hz和60 Hz下进行规定，而且CMRR通常针对的是直流值。两个参数的典型值分别大于80 dB和120 dB。

• DMM的显示位数与分辨率无关，但有助于确定可以显示和读取的有效位数。 
• 对于大多数应用来说，阻抗越高，电压测量就越准确。
• 波峰因数越高，波峰越尖锐，要获得准确的交流测量值也就越困难。
• 偏移量归零有助于消除直流电压或电阻测量时由于连接和导线引起的误差。
• 自动调零用于补偿仪器内部的偏移。
• 电流测量要求断开电路，以便将DMM插入电路回路。 
• 在电流模式下，意外测量电压会导致保险丝熔断。
• 电路断电时，适合进行电阻测量和连续性测试。
• 常模抑制比(NMRR)描述了DMM对出现在两个输入端之间的噪声的抑制能力。
• 共模抑制比(CMRR)描述了DMM抑制两个输入端公共噪声的能力，如来自嘈杂环境的噪声。