Managing FPGA Deployments
Overview
One of the primary advantages of an FPGA is the ability to load different hardware personalities based upon the needs of specific applications. However, because of the FPGA’s flexible nature, it is important to ensure that the correct practices are used for tasks such as development, stand-alone deployment and maintenance. This article will address best-practices for each of these phases in the development lifecycle within the LabVIEW environment.
Contents
- Managing FPGA Files on Disk
- Validating FPGA Logic During Development
- Deploying Stand-alone FPGA Applications
- Mass Deployment of FPGA Application
- Maintaining Existing FPGA Applications
- Best-practices summary
Managing FPGA Files on Disk
A LabVIEW FPGA application is developed in a VI that is targeted for a specific NI FPGA device. The FPGA VI in turn goes through a compilation process that eventually generates a bitfile, which when downloaded to the FPGA configures it to function as specified in the VI. If an FPGA is modified, it must be recompiled which overwrites the bitfile that is stored on the development machine. As a result, it is important that a versioning system is in place to account for both the FPGA VI as well as the bitfile.
Since the FPGA VI is where the application is programmed, it is often incorporated in a source code control system. Although the bitfile cannot be opened to reference the logic of the application it should also be included in a versioning system because it provides a compiled static file that can be referenced back to throughout the software development process.
If bitfile versioning is implemented the bitfile should be renamed to a meaningful value before it is submitted to source code control for ease of reference. By default, the bitfile is in a folder called “FPGA Bitfiles” at the same level as the FPGA VI. To verify the location of the bitfile complete the following step:
- Navigate in the LabVIEW Project Explorer window to the FPGA VI, right-click on it and select Target-specific Properties…
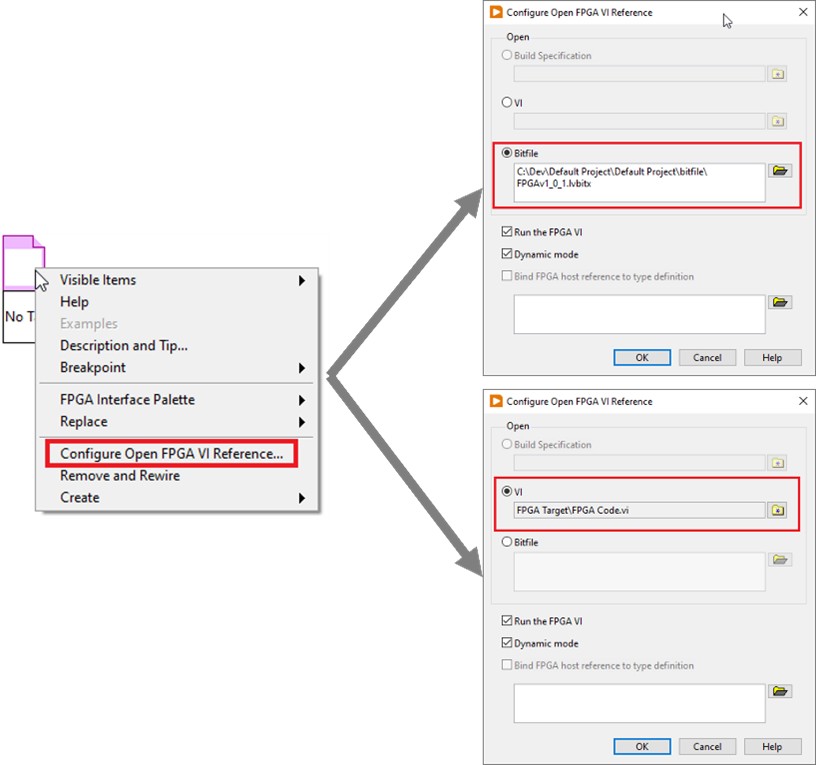
The way in which an FPGA application is referenced in a host application will depend on the versioning that is implemented in a system. To reference a specific FPGA VI version, it will need to be checked out of source code control and then the host VI’s “Open FPGA Reference” function will need to be updated to point to the VI as shown in Figure 1. If the bitfile is referenced for versioning the “Open FPGA Reference” then should be updated to point to it rather than the FPGA VI.
Figure 1: The Open FPGA VI Reference can be configured either to reference the bitfile or the FPGA VI.
Validating FPGA Logic During Development
In the course of developing an FPGA VI the program logic must often be tested to validate its operation. Using the interactive front panel communication method, in which the run button is asserted for an FPGA VI in the development environment, is one way to test the operation of the application. However, this process involves a complex compilation process to convert the LabVIEW FPGA VI to a bitfile and then deploy it to the target which may take anywhere from a few minutes to multiple hours. In addition, it requires that the developer has the target device available to deploy the FPGA application.
As an alternative to recompiling and deploying a new application for each test, the LabVIEW FPGA module includes an FPGA simulation environment in which the application can be run on the development machine. This allows the validation of the overall application logic before the time intensive compilation process is undertaken. Furthermore, since it runs on the development machine the actual hardware is not required to run an FPGA simulation. To find out more information on simulating an FPGA target in LabVIEW reference the Efficient Development and Debugging with LabVIEW FPGA Developer Zone article.
It is important to note that interactive front panel communication should only be used for the development phase of an FPGA application as the configuration on the FPGA is volatile. When the bitfile is downloaded to the FPGA it will be lost if the device is power cycled, therefore another method is required for stand-alone deployments.
Deploying Stand-alone FPGA Applications
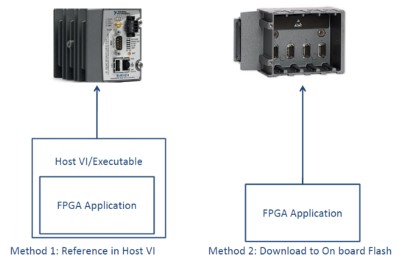
Once the development phase of the FPGA application is complete the generated bitfile, also referred to as a personality, needs to be deployed to the system. The way in which the file is deployed will depend on whether the FPGA is independent or dependent on a host VI. If the FPGA VI does require communication or data logging, then the development of a host VI is required. However, if the FPGA runs independently of any other target, then the personality should be stored in non-volatile flash memory on the FPGA target. The relationship between these two deployment methodologies and where the FPGA personality is then stored for a CompactRIO is displayed in Figure 2.
Figure 2: The two stand-alone deployment methodologies.
Method 1: Referencing the FPGA in a Host VI
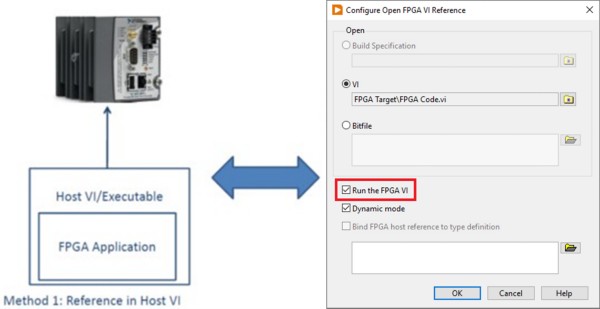
The most prevalent method for deploying an FPGA personality is to embed it into the host application as shown in Figure 3. This inclusion into the application occurs when the “Open FPGA Reference” function is used in the host implementation. When the host application is then compiled into an executable the FPGA application is embedded inside this file. Therefore, when the host application is deployed and run, it will download the bitfile and open a reference to the FPGA when the “Open FPGA Reference” function is called.
Figure 3: If an Open FPGA VI Reference is used in a Host VI then the FPGA’s bitfile is embedded into the host file.
Since the bitfile is embedded into the executable, a benefit of this method is that it includes both targets’ application into one file. In addition, since the host file is an executable, it can simply be transferred to the host using any FTP program.
It is worth noting that the host application is required to initialize before the FPGA application is loaded and as a result there is a delay from device power up to the configuration of the FPGA. In addition, on power up the state of the input and output lines of your target will be unknown since the FPGA has not yet been configured. Therefore, if the FPGA is completely independent of the host application, its personality should be stored in the on-board FPGA flash.
Method 2: Storing the application in non-volatile flash memory on the FPGA target
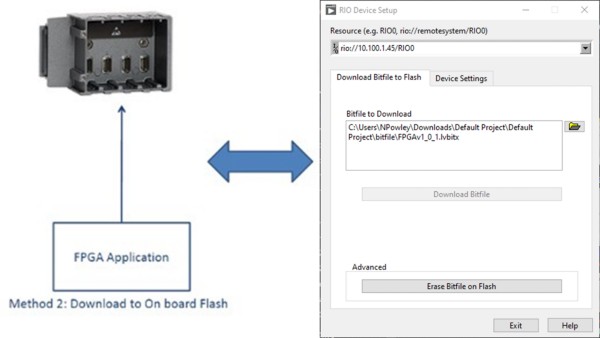
The bitfile can also be downloaded to flash memory on the FPGA target device using the “RIO Device Setup” that is included with the NI-RIO driver as shown in Figure 4. Subsequently, whenever the target is rebooted, it immediately loads the personality onto the FPGA from the flash independent of what the host application is executing. In addition, downloading the personality to the flash ensures that when the device is power up it drives all of the input and output lines to a known state since it is loaded immediately on to the FPGA.
Figure 4: The FPGA bitfile can be downloaded to the FPGA’s on-board flash using the RIO Device Setup.
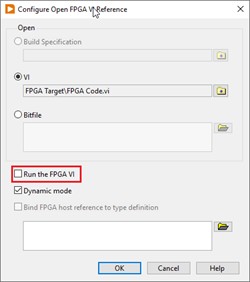
If communication does occur with the host, the host application will have to be modified so that the “Open FPGA Reference” function does not overwrite the personality that is automatically loaded onto the FPGA. To disable this download, uncheck the “Run the FPGA VI” option in the “Open FPGA Reference” function configuration, as shown in Figure 5. In addition, since the FPGA personality is loaded immediately on boot up from the flash the connecting host does not immediately have control over the current state of the FPGA. If host control of the FPGA is needed, the personality should be embedded into the host application rather than stored in flash.
Figure 5: The “Run the FPGA VI” option in the Open FPGA VI Reference configuration window will need to be disabled if the FPGA bitfile is loaded from the on-board flash so that the host application does not overwrite the bitfile on the FPGA.
The recommended personality deployment architecture will depend on the needs of the specific application. However, in most implementations it is recommended that the personality is embedded in the host application since the FPGA often is dependent on a host application.
Mass Deployment of FPGA Application
To deploy many FPGA based systems in which the on-board flash is utilized to store the personality, it becomes impractical to manually load the personality on to each device. With the Replication and Deployment (RAD) Utility you can use RAD to replicate the image of a real-time target to make deployment of targets and systems more efficient.
If the personality is embedded into the host application the personality will be transferred with the executable. As a result, if many of these systems need to be deployed the Real-Time Target System Replication or the Windows based installer can be utilized to automate the deployment process.
Maintaining Existing FPGA Applications
Often a deployed target’s image will need to be updated with a modified version of the personality. This redeployment process can be accomplished identically to the initial deployment by overwriting the files on the target; however, environment variables such as deployed location may impede this deployment procedure. Both the RIO Device Setup application and FTP applications are setup to address this transfer of files across a network.
If there is no network available at the remote location and the FPGA personality is embedded in the host VI, a technician’s machine only needs FTP capabilities to transfer the update to the host. If the personality is stored on the FPGA on board flash, the machine at the remote location will require that the NI-RIO driver is installed in order to utilize the RIO Device Setup application.
Best-practices summary
- Backup both FPGA VIs and bitfiles in order to establish a versioning system
- Validate FPGA logic by simulation on development PC rather than compiling and deploying to the actual target each time
- Use the interactive front panel communication deployment method only during development
- Develop a host application, in which the FPGA bitfile will be embedded, if they are dependent on one another otherwise download the application to the on board flash
- In order to mass deploy an FPGA application use the Replication and Deployment (RAD) Utility if the application is downloaded to the onboard flash
- Use the same method for maintenance deployment as for the initial deployment