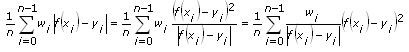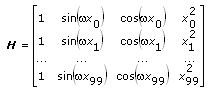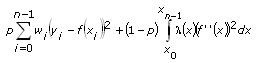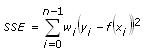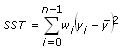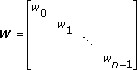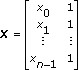LabVIEWにおけるカーブフィットモデルと方法の概要
概要
テスト/計測の現場では、観測値と独立変数の数学的関係が存在することが多々あります。例えば、温度の計測データ、観測可能な値、および計測誤差(不正確な計測デバイスで得られる独立変数)の間にある相関関係などです。数学的関係を求める1つの方法はカーブフィット(曲線近似)です。この方法では、観測値に合った適切な曲線を定義し、曲線の関数を使用して変数同士の関係を解析します。
カーブフィットすることで、次のようなことができます。
- ノイズを軽減して、データを平滑化する
- サンプル同士の数学的関係または関数を求めて、誤差補正、データ処理、速度および加速度の計算などのデータ処理を行う
- サンプル値とサンプル値の間の値を見積もる(内挿)
- サンプルした値範囲外の値を見積もる(外挿)
この技術資料では、さまざまなカーブフィットモデル、方法、およびカーブフィットに使用できるLabVIEW関数について説明します。
内容
LabVIEWにおけるカーブフィット
カーブフィットとは
カーブフィットの目的は、i=0, 1, 2,…, n–1の場合のデータ(xi, yi)に対して、Wで重み付けされた残差を最小化するような関数f(x)を求めることです。関数f(x)は、最小化することです。残差が少ないということはつまり良く近似できているということです。幾何学的な表現をすると、カーブフィットは、i=0, 1, 2,…, n–1の場合のデータ(xi, yi)に合うような曲線y=f(x)を見つけることです。
多くの計測/解析ソフトウェアにはカーブフィットのための機能が搭載されており、テストエンジニアが手作業で近似する曲線を求める必要はありません。例えば、LabVIEWでは、次のVIを使用して、カーブフィット関数を求めることができます。
- 線形フィットVI
- 指数フィットVI
- 累乗フィットVI
- ガウスピークフィットVI
- 対数フィットVI
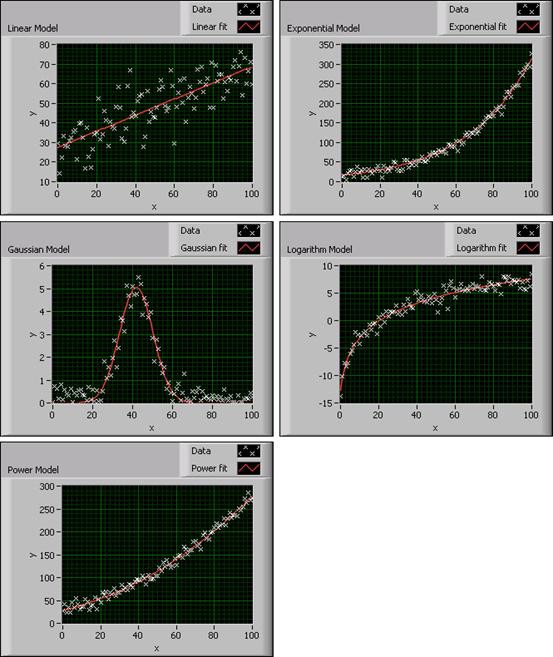
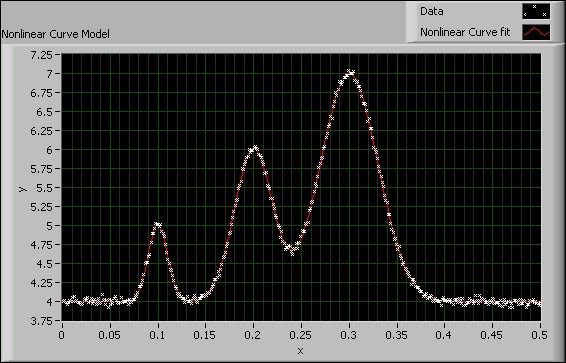
これらのVIは、データセット(データ値の集合)に対して異なる種類のカーブフィットモデルを使用します。これらのVIを使用するための詳細については、LabVIEWのヘルプを参照してください。次のグラフは、LabVIEWで作成できる、さまざまなフィットモデルの例です。
図1. LabVIEWのカーブフィットモデル
データセットを近似する前に、使用する近似モデルを決定する必要があります。例えば、対数的な特性を持つデータに対して、線形モデルで近似させようとすると、近似結果が不正確になり、謝ったデータセットの特性を導いてしまいます。したがって、まず、データの分布状態に基づいた適切な近似モデルを選択する必要があります。さらに、近似した結果に従って、このモデルが適しているかどうかを判断する必要があります。
LabVIEWのカーブフィットのモデルには全て、重み付けがあります。重み付けのデフォルト値は1です。この場合、全てのデータサンプル値が、フィットの結果に同じ影響を受けます。場合によっては、ノイズなどの外部要素のせいで、データセットに外れ値があります。データサンプル値と同じ重み付けで外れ値を計算した場合、フィットの結果に悪影響が出ます。したがって、重みを0に設定したりして、外れ値の重みを調節することによって、この種の影響を排除することができます。
また、LabVIEWのカーブフィットExpress VIを使用して、カーブフィットアプリケーションを開発することもできます。
カーブフィットの方法
カーブフィットの方法にはいくつかの種類があり、それぞれ異なった方法で、入力データを評価して、カーブフィットモデルのパラメータを求めます各方法ごとに、近似した曲線を求める際、残差の評価に対する独自の基準があります。各方法の基準を理解することによって、最も適切な方法を選択し、曲線を近似することができます。LabVIEWでは、最小二乗法(LS)、最小絶対残差法(LAR)、または二重平方近似法を線形フィット、指数フィット、累乗フィット、ガウスピークフィット、または対数フィットVIに適用して、関数f(x)を求めます。
最小二乗法では、次の式に従い、残差を最小化することによって、f(x)を求めます。
nはデータサンプルの数です。
wi は、データサンプルに対する重みのi番目の要素です。
f(xi)は、フィットモデルの数あるy値のi番目の要素です。
yiは、データセット(xi, yi)のi番目の要素です。
最小絶対残差法では、次の式に従い、残差を最小化することによって、f(x)を求めます。
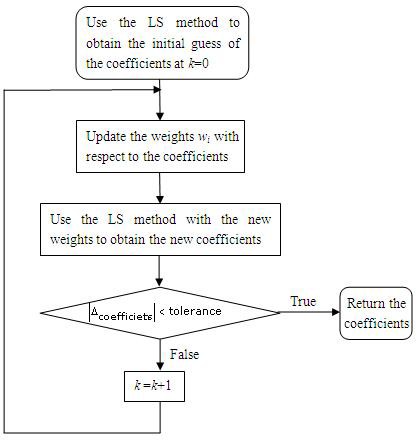
二重平方法では、次のフローチャートに示したような反復プロセスを使用してf(x)を求め、最小二乗法で使用するのと同じ式を用いて残差を計算します。二重平方法では、反復kから開始するデータを計算します。
図2. 二重平方フローチャート
最小二乗法、最小絶対残差法、および二重平方法がf(x)を異なった方法で計算するため、データセットに応じて使用する方法を選ぶ必要があります。例えば、最小絶対残差法および二重平方法は、ロバストな(ノイズなどの外乱に影響されにくい)近似方法です。外れ値がデータセットにある場合、これらを使うのがよいでしょう。続いて、最小二乗法、最小絶対残差法、二重平方法の計算方法を見ていきましょう。
最小二乗法
最小二乗法は、次の一次方程式を解くことから始めます。
Ax = b
ここでAは行列で、xとbはベクトルです。Ax–bは、この式の残差を表します。
次の式は、上記の式の二乗誤差を表します。
E(x) = (Ax-b)T(Ax-b) = xTATAx-2bTAx+bTb
二乗誤差E(x)を最小化するには、上記の関数を微分したものが、結果を0になる場合を考えます。
E’(x) = 0
2ATAx-2ATb = 0
ATAx =ATb
x = (ATA)-1ATb
このアルゴリズムは、反復する演算がないので、計算量が少なく、効率が良いことがわかります。効率の良さを必要とするアプリケーションには、この方法が適しています。
最小二乗法は、二乗誤差の最小化とガウス分布ノイズを持つデータの処理によってxを算出します。ノイズがガウス分布ではない場合(例えば、データに外れ値がある場合など)、最小二乗法は適していません。最小絶対残差法メソッド、二重平方法など、別の近似方法を使用すれば、非ガウス分布のノイズを含むデータを処理できます。
最小絶対残差法
最小絶対残差法は次の式に従って残留を最小化します。
この式から、最小絶対残差法は重みの変わる最小二乗法であることが言えます。データサンプル値がf(x)から程遠い場合、重みは繰り返しごとに、比較的低く設定されます。そうすれば、このデータサンプル値がフィットの結果に与える悪影響が小さくなります。したがって、最小絶対残差法は外れ値のあるデータに適しています。
二重平方法
最小絶対残差法と同様、二重平方法も繰り返し演算によって、データサンプル値の重みを変更します。ほとんどの場合、二重平方法は、最小絶対残差法と比べて外れ値に影響されません。
カーブフィット方法の比較
3つのカーブフィットを比較すると、最小絶対残差法および二重平方法は、反復プロセスを使用して各データサンプル値の重みを調節することにより、外れ値の影響を軽減していることがわかります。残念なことに、各データサンプル値の重みを調節すると、最小絶対残差法および二重平方法の効率も下がってしまいます。
3つの方法をより良く比較するには、次のように考えます。3つの方法を使用して、同じデータセット(ノイズのある50個のデータサンプル値を持つ線形モデル)を近似させます。次の表は、各方法にかかる計算時間を示しています。
図1. 3つの方法に要する時間
| フィットメソッド | 最小二乗法 | 最小絶対残差法 | 二重平方法 |
| 時間(μ秒) | 3.5 | 30 | 60 |
上記の表から、最小二乗法の効率が最も高いことがわかります。
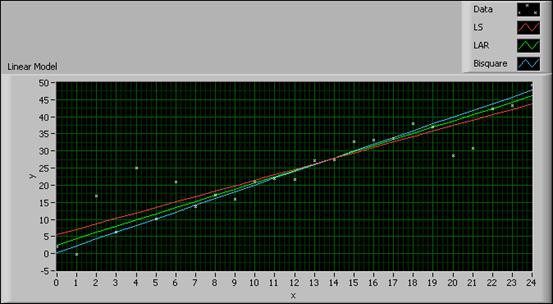
次の図は、3つの方法に与える外れ値の影響を示しています。
図3. 3つの近似方法の間での比較
近似曲線から離れたところにあるデータサンプル値が外れ値です。上記の図では、(2, 17)、(20, 29)、および(21, 31)に位置するデータサンプル値は外れ値と見なすことができます。この結果から、外れ値の影響が、最小絶対残差法および二重平方法と比べて最小二乗法に大きく及んでいることがわかります。
以上より、適切な近似方法を選択する場合、データの質と計算の効率の両方を考慮する必要があるということがわかります。
LabVIEWカーブフィットモデル
線形フィット、指数フィット、ガウスピークフィット、対数フィット、および累乗フィットVIの他に、次のVIを使用して、カーブフィット関数を計算することもできます。
- 生成多項式VI
- 一般LS線形VI
- 3次スプラインフィットVI
- 非線形カーブフィットVI
一般多項式フィット
一般多項式フィットVIは、次のようにデータセットを一般化された多項式関数にフィットさせます。
f(x) = a + bx + cx2 + …
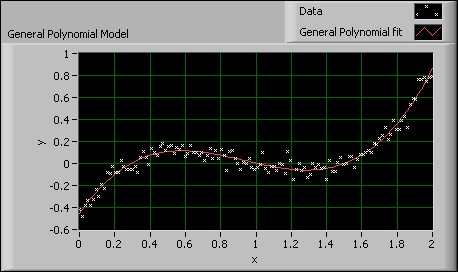
次の図は、3次多項式を使用して零点を通る近似曲線を示しています。f(x)がy=0を通過するのがおよそ(0.3, 0)、(1, 0)、および(1.5, 0)のあたりだということがわかります。
図4. 一般多項式モデル
このVIは次の式を使用して平均二乗誤差(MSE:Mean Square Error)を計算します。
一般多項式フィットVIを使用する際、最初に多項式の次数を設定する必要があります。多項式の次数が高ければ、良い近似ができるとは限らず、解の発散の原因になります。ほとんどのアプリケーションでは、10次以下の多項式での要件を満たすことができます。多項式次数のデフォルト値は2です。
このVIには、係数制約の入力があります。多項式係数の正確な数値を知っている場合、この値を設定することができます。この入力を設定することによって、VIは、正確な数値により近い係数を算出することができます。
一般LS線形VI
一般LS線形フィットVIは、次の式に従ってデータセットを近似します。
y = a0 + a1f1(x) + a2f2(x) + …+ak-1fk-1(x)
yは係数a0, a1, a2, …, ak-1の線形結合で、kは係数の個数です。
次の式は、係数の線形結合の式において、a1の乗数をxの関数として表しています。
y = a0 + a1sin(ωx)
y = a0 + a1x2
y = a0 + a1cos(ωx2)
ここでωは角周波数です。
上記の各式で、yは係数a0とa1の線形結合です。一般LS線形フィットVIの場合、yは複数の係数の線形結合でもあります。各係数にはx.の関数の乗数があります。したがって、一般LS線形フィットVIを使用して、この関数の係数を係数の線形結合として表記できます。
y = a0 + a1sin(ωx)
y = a0 + a1x2 + a2cos(ωx2)
y = a0 + a1(3sin(ωx)) + a2x3 + (a3/x) + …
上記の各式では、yは係数a0, a1, a2,…の線形関数でもあり、xの非線形関数でもあり得ます。
観測行列の構築
一般LS線形フィットVIを使用する際、観測行列H.を構築する必要があります。例えば、次の式は、トランスデューサからのデータを使用してモデルを定義します。
y = a0 + a1sin(ωx) + a2cos(ωx) + a3x2
次の表は、上記の式の係数aの乗数を示しています。
|
係数 |
乗数 |
|
ao |
1 |
|
a1 |
sin(ωx) |
|
a2 |
cos(ωx) |
|
a3 |
x2 |
観測行列Hを構築するため、Hの各列の値は独立関数、またはベクトルxの個々の値xiに等しくなっています。次の式では、上記の式を使用して、100個のxの値を含むデータセットに対する観測行列Hを定義します。
データセットに、係数a0, a1, …, ak– 1に対するn個のデータポイントおよびk個の係数が含まれている場合、Hは、n × kの観測行列になります。したがって、H の行数は、データポイントnの数に等しくなります。Hの列数は係数kの数と等しくなります。
係数a0, a1, …, ak – 1を得るために、一般LS線形フィットVIによって、次の一次方程式を解きます。
H a = y
ただしa = [a0 a1 … ak – 1]Tおよびy = [y0 y1 … yn – 1]T
3次スプラインフィットVI
スプラインとは、データを補間および平滑化するための区分的多項式関数です。カーブフィットでは、スプラインで複雑な形の近似曲線を描くことができます。
3次スプラインフィットVIでは、次の式の値を最小化することによって、データセット(xi, yi)を近似します。
ただし、pはバランスパラメータとします。
wi はデータセットに対する重みベクトルのi番目の要素、
yiはデータセット(xi, yi)のi番目の要素、
xiはデータセット(xi, yi)のi番目の要素、
f"(x)は、3次スプライン関数f(x)の2階微分です。
λ(x)は区分的定数関数です。
λiは、「スムーズさ」を表す入力のi番目の要素です。
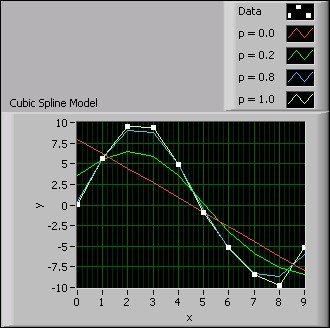
バランスパラメータ入力pが0の場合、3次スプラインモデルは線形モデルに等しくなります。バランスパラメータ入力pが1の場合、フィットメソッドは3次スプライン補間に等しくなります。近似曲線が観測値に近くなり、平滑化されるためには、pが[0, 1]の範囲内にある必要があります。pがより0に近い場合、近似曲線はよりスムーズに、すなわち平滑化されます。pがより1に近い場合、近似曲線はより観測値に近くなります。次の図は、pの値が異なる場合の近似の結果を示しています。
図5. 3次スプラインモデル
上記の図から、pが1.0の場合、近似曲線は観測データに最も近くなることがわかります。pが0.0の場合、近似曲線は最も平滑化されますが、この曲線はいかなるデータポイントとも重ならない場合があります。
非線形カーブフィット
非線形カーブフィットVIは、非線形レーベンバーグ・マルカートメソッドを使用し、次の式に従って、データを曲線近似します。
y = f(x; a0, a1, a2, …, ak)
a0, a1, a2, …, akは係数で、kは係数の数です。
非線形レーベンバーグ・マルカートメソッドは、最も一般的な曲線近似の方法で、yがa0, a1, a2, …, akと線形関係である必要がありません。非線形レーベンバーグ・マルカートメソッドを使用して、線形または非線形な曲線に近似させることができます。しかし、このメソッドの最も一般的な適用は、非線形な曲線に近似させることです。一般的な線形近似は、線形な曲線に近似するのに適しているからです。
また、LabVIEWには、制約付き非線形カーブフィットVIもあり、制約付きの非線形曲線に近似させることができます。各フィットパラメータの上限と下限をデータセットに関する予備知識に基づいて設定して、より良いフィットの結果を得ることができます。
次の図は、非線形カーブフィットVIをデータセットに使用したところを示しています。データセットの非線形性は、非線形レーベンバーグ・マルカートメソッドを適用するのに適しています。
図6. 非線形カーブモデル
前処理
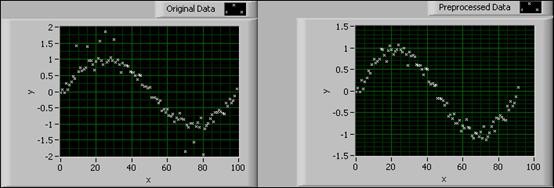
外れ値を削除VIは、範囲外にはみ出したデータポイントを削除することによってデータセットを前処理します。このVIは、外れ値が目的関数に及ぼす影響を取り除きます。次の図は、外れ値を削除VIの適用前と適用後のデータセットを示しています。
図7. 外れ値を削除VI
上記の図では、左のグラフが外れ値のある元のデータセットを示しています。右の図は、外れ値を削除した後の前処理済みのデータを示しています。
また、ユーザが指定した配列指標内に入る外れ値を削除することもできます。
一部のデータセットは、高度な前処理を必要とします。中央値フィルタの前処理ツールは外れ値の削除とデータの平滑化の両方に役立ちます。
後処理
LabVIEWには、カーブフィット実行後のデータ結果を評価するVIがあります。これらのVIは、カーブフィットの結果の正確性を判断し、一連の計測の信頼区間および予測区間を計算することができます。
フィット(近似)の適合度
フィットの適合度VIは、フィットの結果を評価し、残差二乗和(SSE:Sum of Squares Error)、R二乗誤差(R2)、二乗平均平方根誤差(RMSE:Root Mean Squared Error)をフィットの結果に基づいて計算します。これらの3つの統計値は、近似モデルが元のデータセットにどれだけ一致しているかを表します。次の式はそれぞれSSEとRMSEを表しています。
ここでDOFは自由度です。
SSEおよびRMSEは、さまざまな要素の影響を反映して、データセットとフィットモデルの違いを表します。
次の式はR二乗を表しています。
ここでSSTは次式による二乗の合計です。
R二乗は、近似結果を定量的に表したものです。R二乗値が高いと、近似モデルがデータセットにより良く近似できているという意味です。R二乗は、SSEとSSTの分数表現のため、値は0と1の間になります。
0 ≤ R-square ≤ 1
データのサンプルが近似されたカーブに正確に一致するとき、SSEは0で、R二乗は1です。一部のデータサンプルが近似曲線から外れているとき、SSEは0より大きく、R二乗は1より小さくなります。R二乗が正規化されているため、R二乗が1に近ければ近いほど、近似レベルが高くなり、曲線の平滑化が小さくなります。
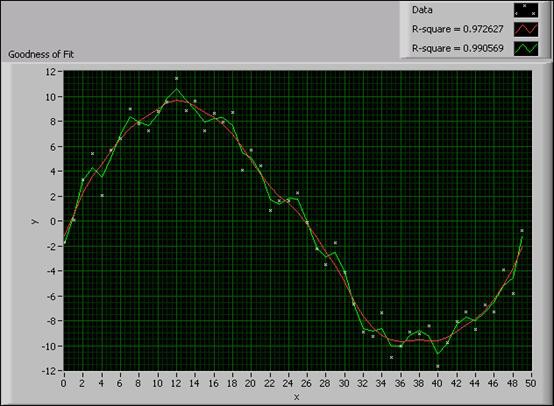
次の図は、異なるR二乗の結果ごとに、データセットに近似させた曲線です。
図8. 異なるR二乗の値による近似の結果
上記の図から、R二乗が0.99の場合の近似曲線はデータセットの値により近くなり、R二乗が0.97の場合より平滑化されていないのがわかります。
信頼区間および予測区間
実際のテスト/計測においては、実験ごとにデータのサンプルは、計測誤差によって異なるため、近似の結果も異なってきます。例えば、計測誤差が全ての実験の間で相互関係を持たず、また一様に分布しない場合、信頼区間を使用して、近似に使用するパラメータの不確かさを推定することができます。また、予測区間を使用して、データセットの従属値の不確かさを推定することもできます。
例えば、線形フィット関数y = a0x + a1に対して、サンプルセット(x0, y0), (x1, y1), …, (xn-1, yn-1)があるとします。各データサンプル(xi, yi)に対して、重み付けによって計測誤差の分散を指定します。
最小二乗法の関数形式x = (ATA)-1ATbを使用して、次の式に従ってデータをフィットさせることができます。
ここではa = [a0 a1]Tです。
また、y = [y0 y1 … yn-1]Tです。
パラメータa0およびa1の共分散行列は次の式のように書き直すことができます。
ここでJはヤコビ行列です。
mはパラメータの個数、
nはデータサンプルの個数です。
上記の式で、パラメータmは2です。i番目のC, Ciiの対角要素はパラメータai, の分散です。
信頼区間では、一定の信頼レベルにおけるフィットパラメータの不確かさを推定します。例えば、95%の信頼区間は、近似パラメータの正しい値が95%の確率で信頼区間内に入るということを意味します。i番目の近似パラメータの信頼区間は次のとおりです。
ここで、 は確率
におけるn–mの自由度のステューデントt逆累積分布関数と呼ばれ、
はパラメータaiの標準偏差で、
に等しくなります。
また、一定の信頼レベルにおける各データサンプルの信頼区間を推定することもできます。例えば、95%の信頼区間は、近似パラメータの正しい値が95%の確率で信頼区間内に入るということを意味します。i番目のデータサンプルの信頼区間は次のとおりです。
ここでは、diagi(A)は行列Aのi番目の対角要素を意味します。上記の方程式では、行列(JCJ)Tは、行列Aを表します。
この予測区間では、一定の信頼レベルにおける、次の計測実験のデータサンプルの不確かさを推定します。例えば、95%の予測区間は、次の計測実験で、データサンプルが95%の確率で予測区間に入ることを意味します。予測区間は正しい値の不確かさを反映するだけでなく、次の計測の不確かさも反映するため、予測区間は信頼区間よりも広い範囲になります。i番目のサンプルの予測区間は次のとおりです。
LabVIEWには、線形フィット、ガウスピークフィット、対数フィット、累乗フィットモデルなど、一般的な曲線近似モデルの信頼区間および予測区間を計算するVIがあります。これらのVIは、信頼区間または予測区間の上界および下界を、設定した信頼レベルに従って計算します。
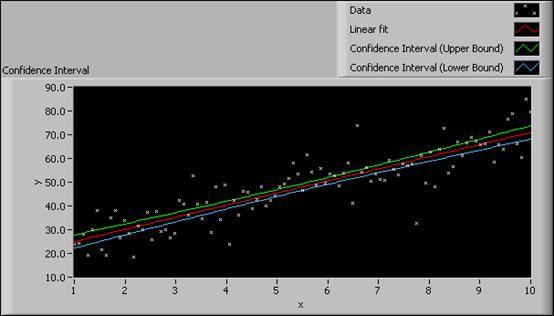
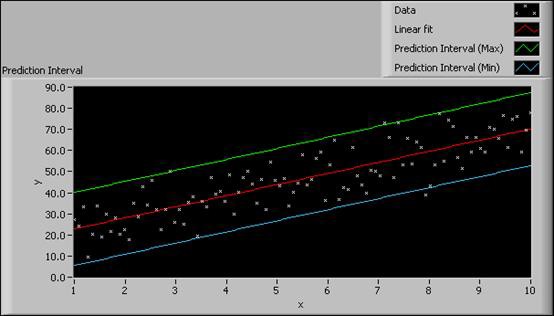
次の図は、同じデータセットに対する信頼区間のグラフと予測区間のグラフそれぞれの例を示しています。
図9. 信頼区間と予測区間
信頼区間グラフからは、信頼区間の幅が狭いことがわかります。小さな信頼区間は、本当のカーブに近い近似曲線であることを示しています。予測区間グラフからは、次の計測実験の各データサンプルが、95%の確率で予測区間内に入ることを結論付けることができます。
アプリケーション例
誤差補正
計測/データ集録機器が古くなると、データ確度に影響する計測誤差が増加します。正確な計測結果を確実に得るためには、曲線近似を使用して、データ誤差を補正する誤差関数を見つけることができます。
例えば、温度計で–50ºC~90ºCの間を計測する実験を検討してみましょう。T1は計測した温度、T2は周辺温度、Teは計測誤差(ここではTe=T1-T2が成り立っている)と仮定します。–50ºC~90ºCの計測可能な範囲内で異なる温度を計測すると、次のようなデータ表が出来上がります。
表2. 周辺温度と計測した温度の読み取り
| 周辺温度 | 計測した温度 | 周辺温度 | 計測した温度 | 周辺温度 | 計測した温度 |
| -43.1377 | -42.9375 | 0.769446 | 0.5625 | 45.68797 | 45.5625 |
| -39.3466 | -39.25 | 5.831063 | 5.625 | 50.56738 | 50.5 |
| -34.2368 | -34.125 | 10.84934 | 10.625 | 55.58933 | 55.5625 |
| -29.0969 | -29.0625 | 15.79473 | 15.5625 | 60.51409 | 60.5625 |
| -24.1398 | -24.125 | 20.79082 | 20.5625 | 65.35461 | 65.4375 |
| -19.2454 | -19.3125 | 25.70361 | 25.5 | 70.54241 | 70.6875 |
| -14.0779 | -14.1875 | 30.74484 | 30.5625 | 75.40949 | 75.625 |
| -9.10834 | -9.25 | 35.60317 | 35.4375 | 80.41012 | 80.75 |
| -4.08784 | -4.25 | 40.57861 | 40.4375 | 85.26303 | 85.6875 |
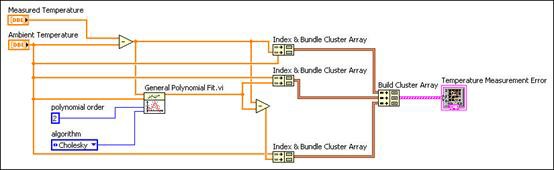
一般多項式フィットVIを使用し、次のブロックダイアグラムを作成して、補正した計測誤差を見つけることができます。
図10. 一般多項式フィットVIを使用した誤差関数VIのブロックダイアグラム
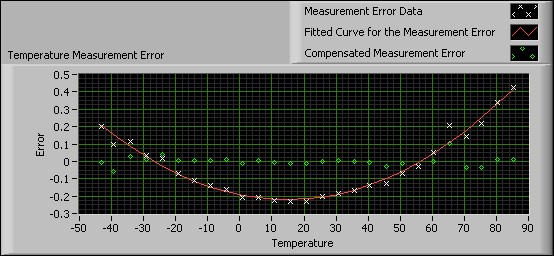
次のフロントパネルは、図10のVIを使用した10回の試行結果を表示しています。
図11. 一般多項式フィットを使用して誤差曲線を近似
上記の図は、元の計測誤差データセット、データセットに近似した曲線、および補正した計測誤差を示しています。データセットに近似した曲線を最初に定義した後、このVIは計測誤差データに近似した曲線を使用して、元の計測誤差を補正します。
この補正された誤差のグラフから、曲線近似を使用することによって、計測誤差が元の誤差値の10分の1にまで減少し、その結果、計測器から得られる結果が改善されることがわかります。
Baseline Wanderingの除去
信号の集録中、信号は低周波数ノイズと混ざり合うことがあり、これがBaseline Wanderingにつながります。Baseline Wanderingは、信号の品質に影響するため、次の試行にも影響が及びます。Baseline Wanderingを除去するため、カーブフィットを使用して、元の信号から信号の傾向を取得し、抽出することができます。
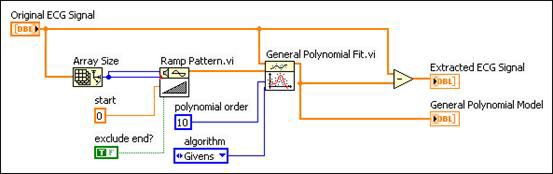
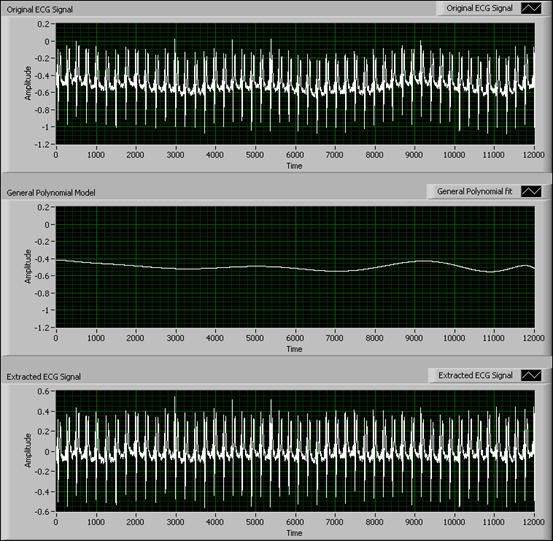
次の図に示すとおり、人間の呼吸を計測するECG信号にBaseline Wanderingを見つけることができます。一般多項式フィットVIを使用して信号の傾向を取得してから、元の信号からBaseline Wanderingを見つけて除去することによって、信号のトレンド除去を行います。残った信号は減算された信号です。
図12. 一般多項式フィットVIを使用してBaseline Wanderingを除去する
上記のグラフから、一般多項式フィットVIを使用することによってBaseline Wanderingを抑えられることがわかります。この例では、曲線近似を使用してBaseline Wanderingを除去するほうが、ウェーブレット解析など、他のメソッドを使用するよりも迅速で簡単です。
エッジ抽出
デジタル画像処理においては、物体の形状を判定してから、その形状のエッジを検出し、抽出する必要が生じることがよくあります。この処理をエッジ抽出と呼びます。照明不足や過剰な照明といった悪条件の下では、不完全なエッジやぼやけたエッジを抽出してしまう場合があります。物体のエッジが正則曲線の場合、曲線近似は最初のエッジを処理するのに便利です。
物体のエッジを抽出するには、まずWatershedアルゴリズムを使用することができます。このアルゴリズムは物体の画像を背景の画像から切り離します。次に、モフォロジーアルゴリズムを使用して、欠如しているピクセルを埋め、ノイズピクセルをフィルタ処理することができます。この物体の形を取得した後、ラプラシアンまたはラプラス演算子を使用して、最初のエッジを取得します。次の図は、部分的に物理的障害のある楕円形の物体の画像に、エッジ抽出プロセスを施しているところです。
図13. エッジ抽出処理の手順
上記の図でわかるとおり、照明条件の悪さと別の物体による妨害のために、抽出したエッジは十分に滑らかではない、あるいは完全ではありません。エッジの形状が楕円のため、最初のエッジの座標を使用して楕円関数に近似させることにより、エッジの質を改善することができます。繰り返し処理をすれば、エッジのピクセルの重みを更新して、最初のエッジの不正確なピクセルの影響を最小化することができます。次の図は、VIのフロントパネルです。これは物体の形状の最初のエッジを抽出し、非線形カーブフィットVIを使用して、最初のエッジを物体の実際の形状に近似させるVIです。
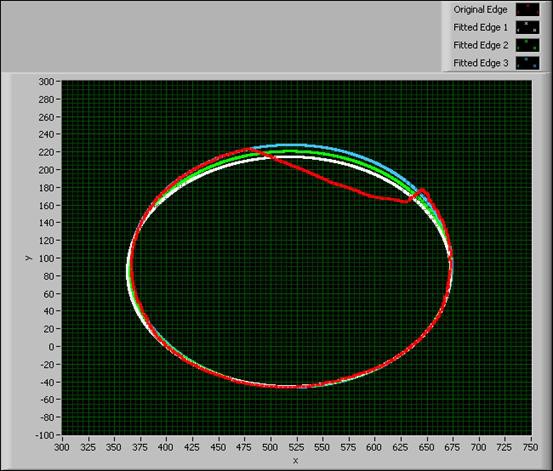
図14. 非線形カーブフィットVIを使用して楕円のエッジに近似させる
上記の図のグラフは、曲線近似させたエッジを計算するための反復の結果です。複数の反復の後、VIは物体の実際の形状に近いエッジを抽出します。
カーブフィットを使用した混合ピクセルの分解
リモートセンシング画像から地上物体を検出するための計測基準は通常、ピクセル単位です。解像度に空間的な制限がかかることによって、1ピクセルが数百平方メートルをカバーする場合もよくあります。ピクセルがさまざまな要素から構成された地上物体を含んでいる場合、それは混合ピクセルです。混合ピクセルは処理が複雑で困難です。混合ピクセルを処理する方法の一つに、水や植物など、対象となる物体の正確なパーセンテージを得る、というものがあります。
次の画像は、2000年7月14日にランドサット7 ETM+が撮影したランドサットの着色像です。この画像は実験データとして、上海領域を映し出しています。
図15.着色像
上記の画像では、ランドサットのマルチスペクトル画像の5つのバンドが確認できます。バンド3は青、バンド4は緑、バンド5は赤です。この画像領域には、3つのタイプの典型的な地上物体が含まれています。つまり、水、植物、そして、土です。土には、建物や橋梁などの人工建築物が含まれます。
一般LS線形フィットVIを使用して、混合ピクセル分解VIを作成することができます。次の図は、一般LS線形フィットVIを使用した分解の結果を示しています。


(a)植物 (b)土および人工建築物 (c)水
図16. 一般LS線形フィットVIを使用して混合ピクセル画像を分解する
ここまでの画像では、黒い領域は対象となる物体が0%であることを示しています。白い領域は対象となる物体が100%であることを示しています。例えば、植物を表している画像では、白い領域が植物の存在を示しています。水を表している画像では、白く波打っている領域が川の存在を示しています。前述の図と図15で、水の表れ方を比較することができます。
この結果から、一般LS線形フィットVIがランドサットのマルチスペクトル画像を正常に3つの地上物体に分解できたことがわかります。
指数関数的に変更したガウスフィット
近似させたいモデルが、LabVIEWに含まれていない場合もあります。例えば、次の式は、指数関数的に変更したガウス関数を表しています。
ここで
y0は、y軸からのオフセット、
Aは、データセットの振幅、
xcは、データセットの真ん中の値、
wは、関数の幅、
t0は、修正係数とします。
LabVIEWのカーブフィットVIは、この関数に直接近似させることができません。LabVIEWでは、一般化された積分を直接計算できないからです。しかし、上記の式の積分は正規確率積分で、誤差関数によって次の式に従って表すことができます。
はLabVIEWの誤差関数です。
指数関数的に変更した元のガウス関数は、次のとおり書き直すことができます。
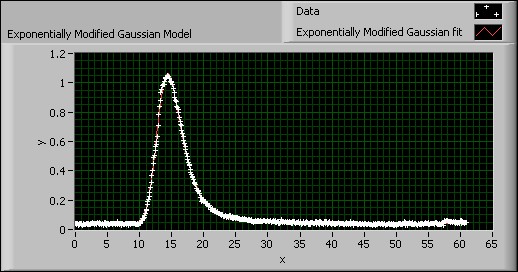
LabVIEWでは、非線形カーブフィットVIを使用して、この式に近似させることができます。次の図は、クロマトグラフィデータに対する指数関数的に変更したガウスモデルを表しています。
図17. 指数関数的に変更したガウスモデル
このモデルは非線形カーブフィットVIおよび誤差関数VIを使用して、指数関数的に変更したガウス関数に最適な曲線に近似します。
適切なVIを使用することによって、新しくVIを作成することができ、LabVIEWにない関数を持つデータセットに対してカーブを近似させることができます。
まとめ
カーブフィット(曲線近似)はデータセットの変数間の関係を評価するだけでなく、ノイズ、不規則性、不正確なテストおよび計測デバイスによる誤差などを含むデータセットの処理も行います。LabVIEWには、最小二乗法、最小絶対残差法、二重平方法など、異なるフィットメソッドを使用する、基本的なカーブフィットVIおよび高度なカーブフィットVIがあり、フィットカーブを見つけることができます。使用する近似モデルおよび近似方法は、近似させたいデータセットによって異なります。また、LabVIEWには処理や評価を行うVIもあり、データセットから外れ値を削除し、近似結果の正確性を評価し、近似させたデータの信頼区間および予測区間を算出できます。
曲線近似およびLabVIEWのカーブフィットVIに関する詳細については、LabVIEWヘルプを参照してください。