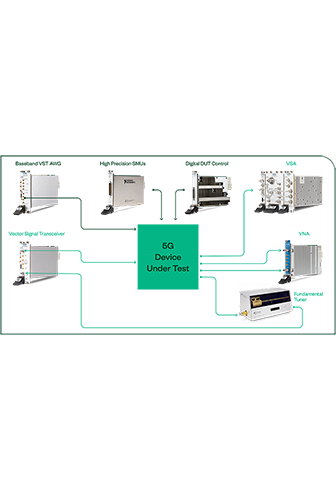
Work with an NI Partner
The NI Partner Network is a global community of domain, application, and test experts working with NI to meet your needs. NI Partners are trusted solution providers, systems integrators, consultants, product developers, and services- and sales-channel experts skilled in a range of industry and application areas.