NI does not actively maintain this document.
This content provides support for older products and technology, so you may notice outdated links or obsolete information about operating systems or other relevant products.
Introduction
Part I of the Understanding Servo Tune document provides information necessary for getting started with tuning servo tune motors. It requires basic knowledge of servo motors, controls, and motion control concepts. This section is dedicated to the basics of servo tuning refer to part II and part III for specific systems.
Part I is divided into the following sections:
GETTING STARTED: ACCESSING SERVO GAIN TUNING
Both the PCI/PXI motion control boards and NI SoftMotion include a gain tuning panel. Depending on your system you will access this through Measurement & Automation Explorer (MAX) or the LabVIEW project. Use the Gain Tuning Panel to determine the relative stability of a servo system and fine-tune the control loop gains. A system is considered stable if the actual position is finite when the commanded position is finite. In other words, a system is stable if a commanded position results in the motor coming to rest at a single position. A system is considered unstable when any commanded position typically results in an exponential increase in position error. In other words, a system is unstable when the attempts to achieve a position result in oscillations that never dampen.
If your system is a 7340 or 7350 PCI/PXI Board follow these steps to access Servo Tune:
The following figure shows the Servo Tune Step Response interface.
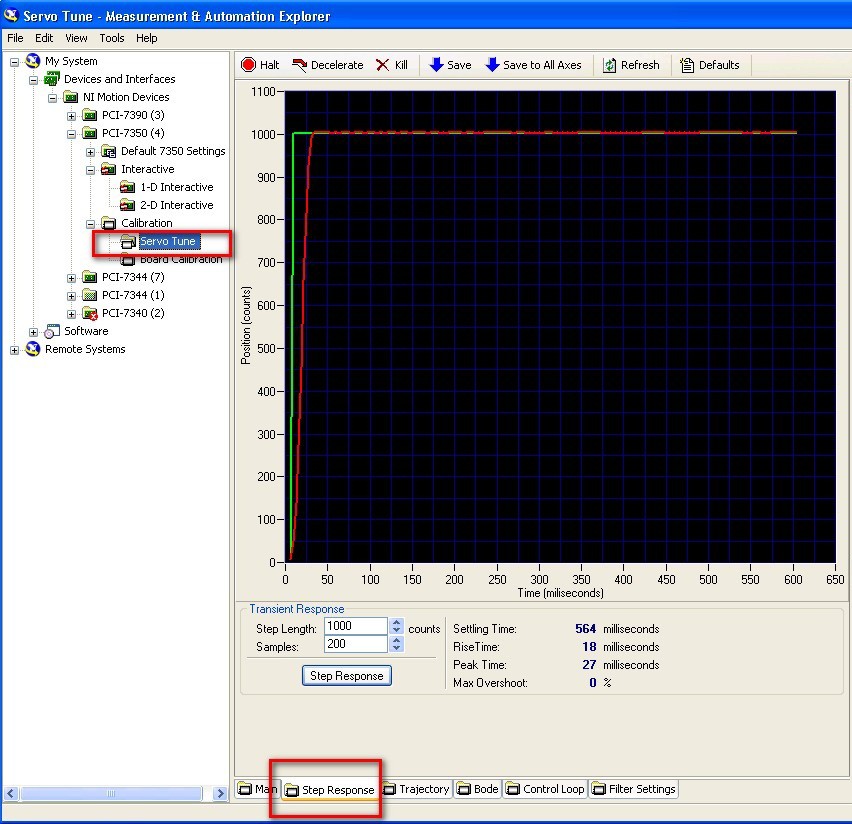
If you are using a NI SoftMotion System follow these steps to access the Gain Tuning Panel:
Note: The following steps walk through setting up a project from scratch if you already have your project setup skip to step 13:
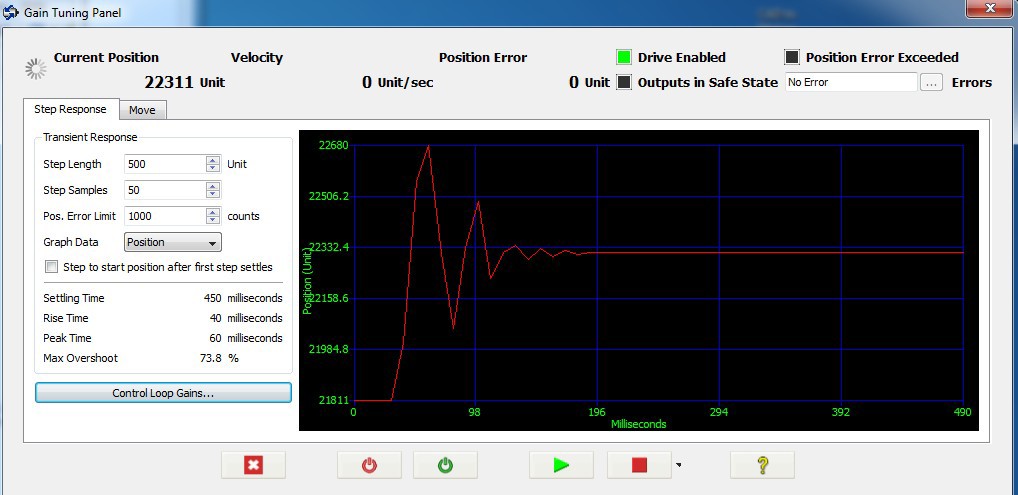
PID CONTROL LOOP PARAMETERS
Proportional Gain (Kp)—Proportional gain is the system stiffness. It determines the contribution of restoring force directly proportional to the position error. Restoring force is comparable to a spring in a mechanical system.
A high proportional gain gives a stiff responsive system but can cause instability from overshooting and oscillation.
Derivative Gain (Kd)—Derivative gain is the damping effects on the system. It determines the contribution of restoring force proportional to the rate of change (derivative) of position error. This force is much like viscous damping in a damped spring and mass mechanical system—a shock absorber, for example.
Increasing derivative gain reduces oscillation at the commanded position, or it rings because of high acceleration.
Integral Gain (Ki)—Integral gain is the static torque load on the system. It determines the contribution of restoring force that increases with time, ensuring that the static position error in the servo loop is forced to 0. This restoring force works against constant torque loads to help achieve zero position error when an axis is stopped.
Integral gain improves positional accuracy. High static torque loads need integral gains to minimize position error when stopped.
STEP RESPONSE
To view your system’s step response, click the Step Response tab in MAX. Use this panel to plot the transient response of your system. Typically, the transient response is measured by first commanding a step, then measuring how quickly a system takes to reach a steady state. Using the transient response, you can calculate the maximum overshoot, rise time, peak time, and settling time of your system.
STABILITY IN THE TIME DOMAIN
Use Step Response to determine the relative stability of the system. A system is considered stable if the actual position is finite when the commanded position is finite. In other words, a system is stable if a commanded position results in the motor coming to rest at a single position.
A system is considered unstable when any commanded position typically results in an exponential increase in position error. In other words, a system is unstable when its attempts to achieve a position result in oscillations that never dampen.
The following figure, taken from the Step Response tab in MAX, shows a typical step response for a servo motor. Following the chart is a description of elements to consider when determining the stability of a servo motor axis.
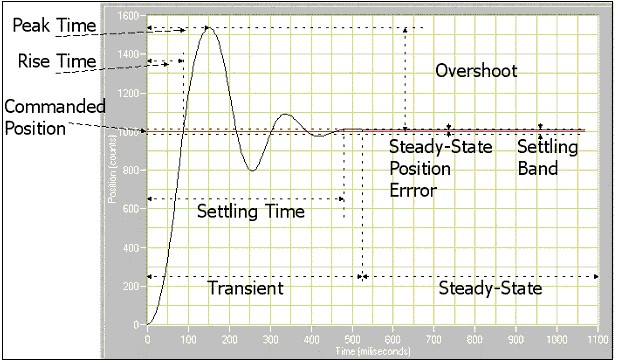
Settling Time—the time required by the response curve to reach and stay within a range that is approximately the final value of size specified by the absolute percentage of the final value (2% to 5%).
Rise Time—the time required by the response to rise from 10% to 90% of its final value; the faster the response time of the system, the faster the rise time.
Peak Time—the time required for a response to reach the first peak of the overshoot.
Maximum Overshoot—the maximum peak value of the response curve measured from the desired position. The maximum overshoot directly indicates the relative stability of the system.
Commanded Position—the desired position. In this case, the commanded position is 1,000 counts from 0.
Steady-State Position Error—the error that occurs when the system is at rest.
Settling Band—the area the position must be within in order to determine settling time.
Note: Part IV of this document outlines what actions to apply in order to modify a Step Response chart and set the system into a stable state.
ANALYZING THE STEP RESPONSE PLOT
This section provides definitions and sample diagrams of the six most common response types.
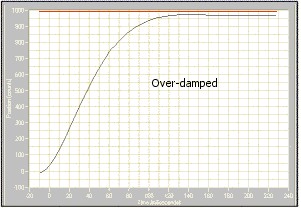
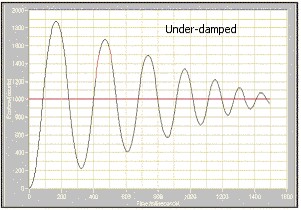
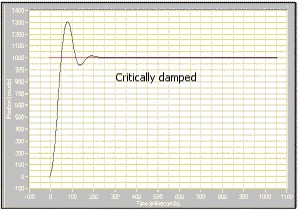
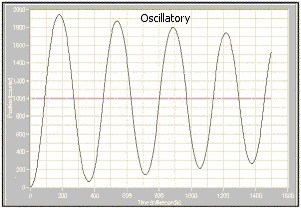
OVERVIEW
Part II of the Understanding Servo Tune document contains guidelines for tuning your system.
Part II is divided into the following sections:
AUTO TUNE OPTIONS
The PCI/PXI 7340 and 7350 boards include an option to automatically tune your servo motors. When automatically tuning your system, use the Control Type and Response Time parameters to customize your system. Smooth controls have a slower response time. The smoother the control, the less the axis will overshoot its desired position before slowing. The more overshoot the system can manage, the faster the response times. Take note that while this may provide a solution in the range that is desired fine tuning using the steps below is still integral to creating a stable system.
TUNING THE SYSTEM
Use the Control Loop tab to view and edit the PID parameters. Auto Tune provides a tuned system, but for an optimally tuned system, it is necessary to fine-tune the final PID parameters. It may also be necessary to alter the PID parameters, depending on your specific circumstances.
PROPORTIONAL GAIN (Kp)
For each sample period, the PID loop calculates the position error and multiplies it by Kp to produce the proportional component of the 16-bit DAC command output. The position error is the difference between the instantaneous trajectory position and the primary feedback position.
An axis with too small a value for Kp is unable to hold the motor in position and is very soft. Increasing Kp stiffens the axis and improves its disturbance torque rejection (its resistance to torque disturbances). However, too large a value for Kp could cause instability.
DERIVATIVE GAIN (Kd)
Every derivative sampling period, the PID loop computes the derivative of the position error. This derivative term is multiplied by Kd every PID sample period to produce the derivative component of 16-bit DAC command output. In order for the servo loop operation to be stable, a nonzero value for Kd is required for all systems that use torque or current amplifiers (where the command output is proportional to motor torque). Small Kd values result in oscillations and servo loop instability.
With velocity or voltage amplifiers in which the command output is proportional to motor velocity, set Kd to 0 or to a very small positive value.
INTEGRAL GAIN (Ki)
For each sample period, the position error is added to the accumulation of previous position errors to form an integration sum. Integration sum is scaled by dividing it by 256 before multiplying it by Ki.
Use the default value (0) for applications with small static torque loads. Static torque loads are those that apply torque to the shaft but are not moving. For systems with high static torque loads, tune this value to minimize position error when the axis is stopped. Ki has no effect when Integration Limit is equal to 0.
DERIVATIVE SAMPLING PERIOD (Td)
The derivative sampling period determines how often (in update samples) the derivative of position error is calculated. Adjust Td for greater flexibility in tuning the PID loop derivative term.
As Td increases, you can use a proportionally lower Kd value for similar results. Start the Td parameter at its default value of 2, and make small adjustments as required by your motion system configuration.
For low inertia systems, set Td to 0 or 1 so that the derivative is calculated often enough to provide adequate damping for servo loop stability.
Systems with higher inertia can benefit from larger Td values. Because higher inertia means that the position error cannot change quickly, it is acceptable to calculate the derivative less often. As a result, you can use a lower Kd value and have the same effective amount of damping, and the system will be smoother with less torque noise from the derivative term. In higher inertia systems, using a Td of 0, and therefore a larger value for Kd, increases torque noise and motor heating without improving system stability.
Tutorial Manually Tuning a System from Scratch
For users of the PCI/PXI 7340 and 7350 you will need to click on the Control Loop tab in MAX to change your coefficients. For those using the LabVIEW NI SoftMotion Module click the Control Loop Gains button located on the Step Response tab of the Gain Tuning Panel. With the Step Response window open you can see the reaction of your system to changes in parameters. Both the PCI/PXI boards and NI SoftMotion follow the same procedure for gain adjustment, perform the following steps to tune your PID control system.


A Tuning Example
The table below provides an example of using this method to quickly tune a servo motor. This example took 20 iterations to arrive at a reasonably well tuned system. The gains used in each iteration are shown as well as the step response graph and characteristics. The screenshots from this tuning are also shown in the animated image of the Step Response window at the beginning of this document.
|
Step
|
Kp
|
Kd
|
Ki
|
Settling Time (ms)
|
Rise Time (ms)
|
Peak Time (ms)
|
Max Overshoot (%)
|
Step Response
|
| 1 |
1
|
0
|
0
|
315
|
96
|
165
|
40
|

|
| 2 |
2
|
0
|
0
|
363
|
57
|
114
|
67
|

|
|
3
|
4
|
0
|
0
|
567
|
39
|
81
|
89
|

|
|
4
|
8
|
0
|
0
|
594
|
27
|
60
|
91
|

|
|
5
|
8
|
1
|
0
|
594
|
27
|
60
|
88
|

|
|
6
|
8
|
2
|
0
|
594
|
30
|
63
|
88
|

|
|
7
|
8
|
4
|
0
|
594
|
27
|
60
|
88
|

|
|
8
|
8
|
8
|
0
|
588
|
30
|
63
|
84
|

|
|
9
|
8
|
16
|
0
|
501
|
27
|
60
|
78
|

|
|
10
|
8
|
32
|
0
|
366
|
30
|
60
|
68
|

|
|
11
|
8
|
64
|
0
|
255
|
30
|
60
|
53
|

|
|
12
|
8
|
128
|
0
|
162
|
33
|
60
|
29
|

|
|
13
|
8
|
256
|
0
|
105
|
45
|
75
|
3
|

|
|
14
|
8
|
192
|
0
|
132
|
39
|
66
|
13
|

|
|
15
|
8
|
192
|
1
|
534
|
42
|
66
|
3
|

|
|
16
|
8
|
192
|
2
|
582
|
36
|
69
|
28
|

|
|
17
|
8
|
192
|
4
|
561
|
36
|
69
|
27
|

|
|
18
|
8
|
192
|
8
|
237
|
33
|
66
|
54
|

|
|
19
|
8
|
192
|
16
|
462
|
30
|
63
|
75
|

|
|
20
|
8
|
192
|
12
|
546
|
30
|
63
|
63
|

|
Note: It is important to note the subtle differences that Kp and Kd have on your system. Increasing Kp increases the slope of the initial rise to the commanded position. As you increase Kp, you approach the commanded position faster, and thus overshoot by a greater amount. Kd reduces the oscillations over a period of time after the initial rise. When Kp decreases, Kd becomes dominant, and when Kd decreases, Kp becomes dominant. When tuning your system, the goal is to find a comfortable balance between Kp and Kd such that there is adequate response time (primarily Kp) and minimal overshoot (primarily Kd), without having to significantly increase or decrease the gains. Increasing or decreasing the gains too much can create an unstable system and possibly damage the motor.
OVERVIEW
Part III of the Understanding Servo Tune document provides information on the advanced features of Servo Tune.
Part III is divided into the following sections:
BODE PLOTS (PCI/PXI 7340 and 7350)
Bode plots are the frequency response of your system. The Bode panel in MAX plots the bode diagram for your system. In order to perform the bode analysis, Servo Tune oscillates the axis to identify the system and to calculate the transfer function. Gain is the measure of the amplitude difference of the input to the system and output from the system. Phase defines the time shift between the input and output. Gain is plotted in decibels (dB), and phase is plotted in degrees.
STABILITY IN THE FREQUENCY DOMAIN
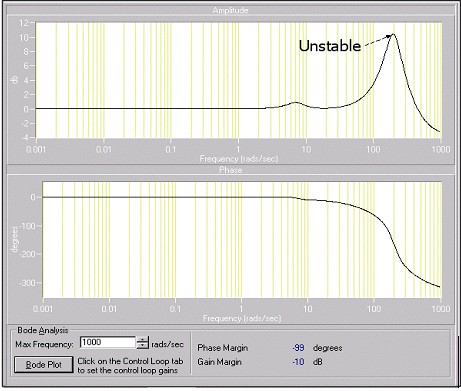
Use bode plots to measure system stability. At low frequencies, the gain is 0 dB for most systems and diminishes as frequency increases. A rise in gain before a fall in gain indicates marginal stability. For most systems, the allowable rise in gain before falling is below 6 dB, indicating approximately 50% overshoot. You can use the bode plots to ensure that at all significant velocities are stable given the PID parameters.
Gain margin is the gain of the system when the phase is at –180 degrees. Phase margin is the difference between the actual phase and –180 degrees when the gain is at 0 dB. Typically, the phase margin should be between 35 and 80 degrees for a stable and responsive system. The phase margin should be as large as possible. The gain margin should be between 10 and 25 dB.
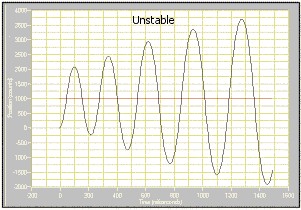
The following graph represents an unstable system. The rise in gain before eventually falling is around 10 dB. This system is unstable at frequencies of approximately 100 radians/sec and higher.
ADVANCED CONTROL LOOP PARAMETERS
The following control loop parameters are often necessary when using velocity or voltage amplifiers.
Velocity Feedback Gain (Kv)
Velocity feedback gain (Kv) is similar to derivative gain (Kd), except that velocity feedback scales only the velocity estimated from the secondary feedback resource. The derivative gain scales the derivative of the position error, which is the difference between the instantaneous trajectory position and the primary feedback position. Like the Kd term, the velocity feedback derivative is calculated every derivative sample period, and the contribution is updated every PID sample period.
When configuring an axis with a secondary feedback encoder, you can use the secondary feedback encoder for velocity feedback. The velocity feedback gain (Kv) scales this velocity feedback before it is added to the other components in the 16-bit DAC command output.
For example, you can use velocity feedback gain for backlash compensation if your system has gears. You can configure the primary feedback to the linear encoder on your system, and the secondary feedback to the rotary encoder on the shaft of the motor. Zero Kd and use Kv instead.
Velocity Feedforward (Vff)
Velocity feedforward determines the contribution in the 16-bit DAC command output that is directly proportional to the instantaneous trajectory velocity. Your system uses this value to minimize following error during the constant velocity portion of a move and can be changed at any time to tune the PID loop.
Because velocity feedforward is an open-loop compensation technique, it cannot affect system stability. However, if the Vff value is too large, the following error during the constant velocity portion can reverse (providing negative following error), which can degrade performance.
Velocity feedforward is rarely used when operating in PID mode with torque block amplifiers. In this case, because the Following Error is proportional to the torque required, and not to the velocity, it is typically much smaller. In this case, velocity feedforward is not required.
Acceleration Feedforward (Aff)
Acceleration feedforward determines the contribution in the 16-bit DAC command output that is directly proportional to the instantaneous trajectory acceleration. Use Aff to minimize Following Error (position error) during acceleration and deceleration, and can be changed at any time to tune the PID loop.
Because acceleration feedforward is an open-loop compensation technique, it cannot affect system stability. However, if the Aff value is too large, following error during acceleration and deceleration can reverse, providing negative following error, which can degrade performance.