LabVIEW FPGA Floating-Point Data Type Support
Overview
Contents
- Single Precision Floating-Point Data Type
- Fixed-Point to Single Precision Floating-Point Data Type Conversion
- Additional Functions with Single Precision Floating-Point Data Type Support
- Single Precision Floating-Point Data Type Development Considerations
- Mixing Fixed-Point and Floating-Point Data Types
- Benchmarking Fixed-Point and Floating-Point Data Types
- Conclusion
Single Precision Floating-Point Data Type
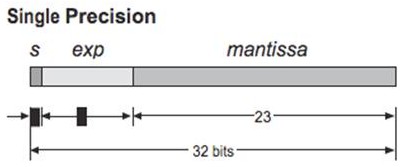
This floating-point format occupies 4 bytes (32 bits) and represents a wide dynamic range of values. In LabVIEW FPGA 2012, this data type is compliant with IEEE Std 754-2008 with the exception of subnormal numbers. The 32 bit base 2 format is officially referred to as binary 32 but, must generally known as single (SGL).
- Sign bit: 1 bit
- Exponent width: 8 bits
- Significand Precision: 23 bits
Figure 1. LabVIEW FPGA 2012 single precision floating-point data type is compliant with IEEE Std 754-2008
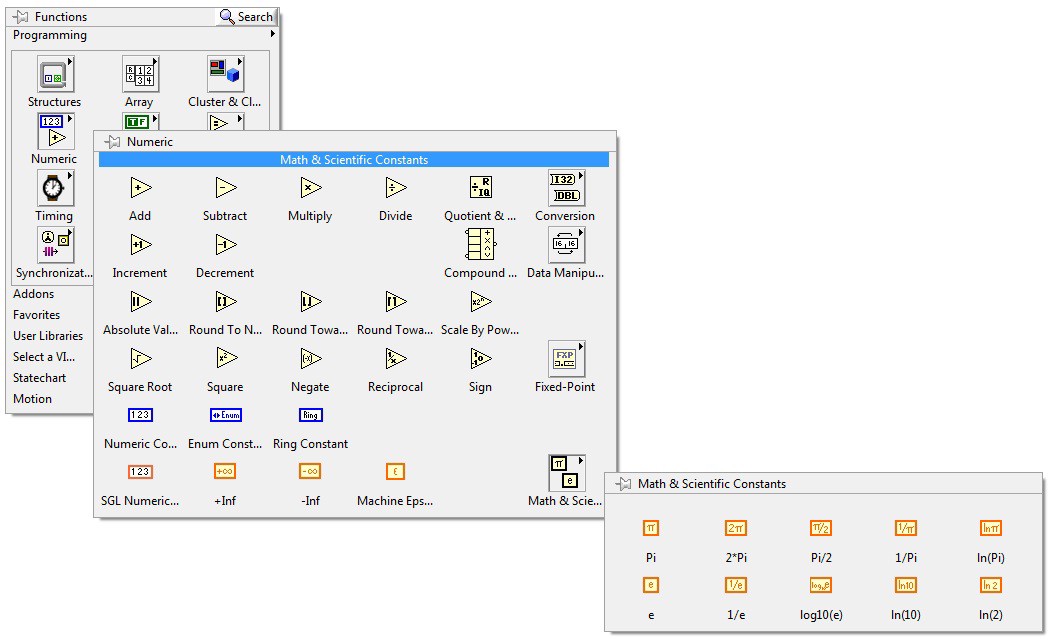
Single precision data type is included in the LabVIEW FPGA Numeric Palette as a SGL numeric constant along with Math & Scientific Constants.
Figure 2. LabVIEW FPGA 2012 exposes a set of single precision floating point data type constants in the numeric palette
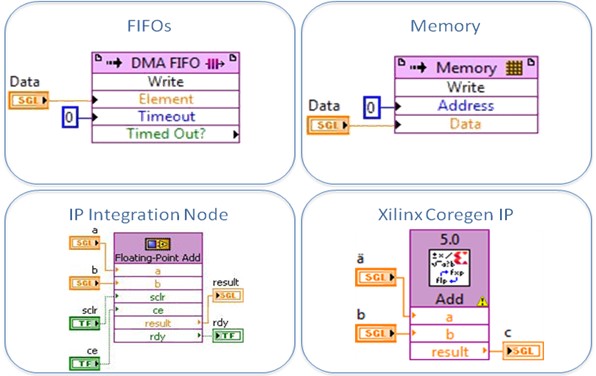
Along with the inclusion of SGL constants, a set of primitives have been optimized for its use with the SGL data type on FPGA. These functions are only suitable for being used outside Single-Cycle Timed Loops (SCTLs). If the code requires the use of a SCTL with floating point operators, the use of the IP Integration Node or the Xilinx Core Generator IP Floating-Point palette is recommended instead.
Figure 3. Single precision floating-point data type supported LabVIEW primitives
Fixed-Point to Single Precision Floating-Point Data Type Conversion
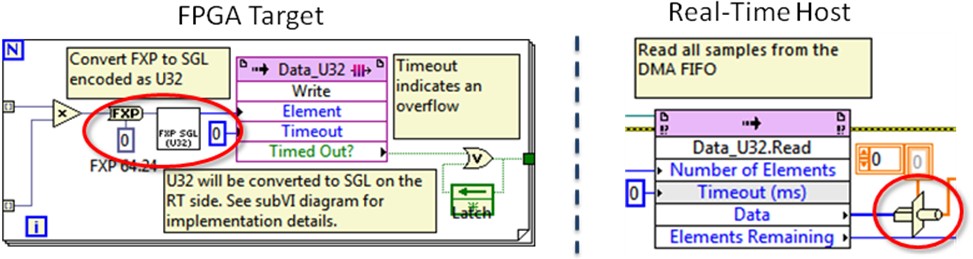
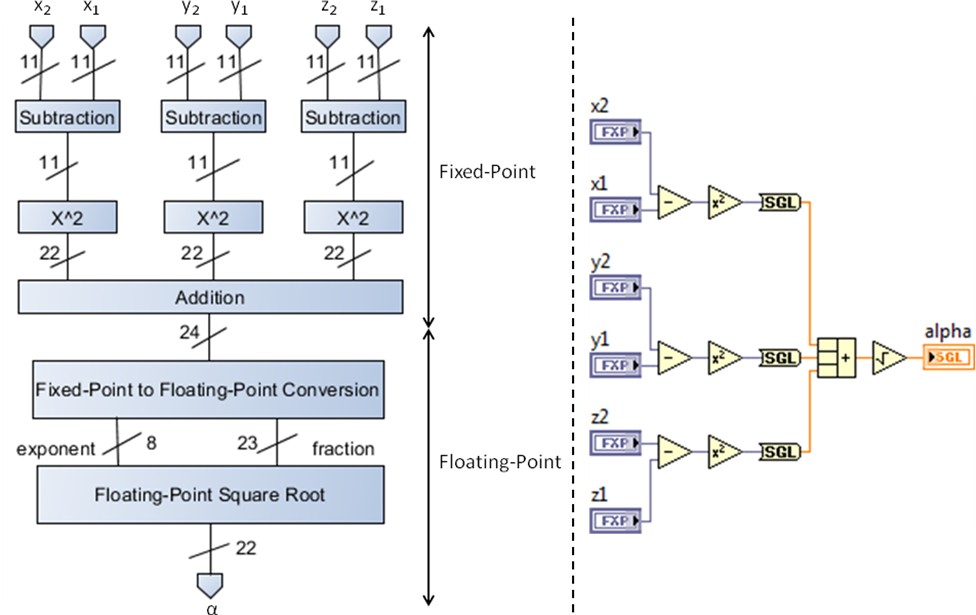
Before LabVIEW FPGA 2012 the use of the floating-point data type was constrained to complicated conversions. This represented extra programming work to perform common instructions such as target-to-host DMA communications and high-throughput mathematics. Conversions from fixed-point to single precision floating-point required to be done by the Host or Real-Time part of the application mostly due to the complexity of implementing this on FPGA. This conversion resulted time consuming if performed on the host side but, still easier to implement than in FPGA. Moreover, performing the fixed-point to floating-point conversion on the host reduced the host’s speed performance up to 40%. The workaround for this issue was to encode the fixed-point data into an integer U32 representation before sending it to the host to lessen the effects of this conversion over the speed execution in the host code. This resulted in extra work to implement the complicated encoding in FPGA, and the host still required a type cast conversion to single precision floating-point. For more detailed information about this process visit the Fixed-Point to Single (SGL) Conversion on LabVIEW FPGA document.
Figure 4. Fixed-point to single precision floating-point conversion performed on FPGA code
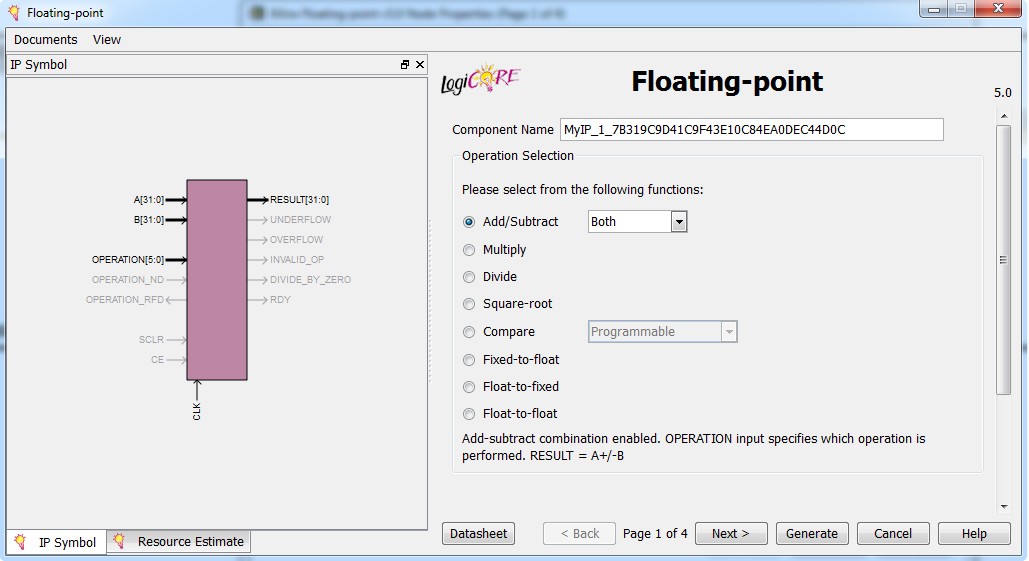
On the other hand, LabVIEW FPGA includes other software development productivity tools such as the Xilinx CORE Generator IP Palette, which makes floating-point implementation feasible through code reuse. This palette includes code that generates IP for conversion to, and basic operations for, floating-point numbers.
Figure 5. The Xilinx Core Generator Floating-Point Operator IP core offers a floating-point function library that can be integrated into LabVIEW FPGA with the Xilinx CoreGEN
LabVIEW FPGA 2012 makes this process even more accessible by introducing the To Single Precision Float function. This function is part of the Conversion palette and allows users to perform single precision floating-point data type operations without involving extra code. This function becomes especially important when it comes to coercions, i.e. automatic conversions that occur in FPGA VIs can consume significant logic resources, especially when the terminal is coerced to the SGL data type. Thus, as a general rule is always advisable to use conversion functions to explicitly convert data types.
Figure 6. To Single Precision Float function can be used to easy perform communications from Target to Host and advanced math operations directly on the FPGA
Additional Functions with Single Precision Floating-Point Data Type Support
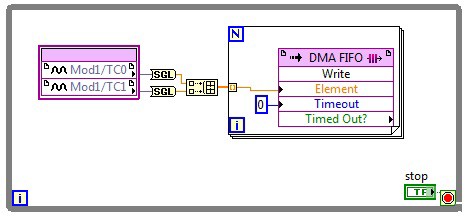
In addition to constants, primitives, and conversion functions, the single precision floating-point is supported in target-scoped, host to target-DMA, target to host-DMA, and peer to peer writer/reader FIFOs. Furthermore, memory elements can be used along with SGL data type in their target-scoped and VI defined implementations. This support is leveraged to elements that were able to perform floating point operations in the past such as the Xilinx Core Generator IP and the IP Integration Node for increased performance and functionality.
Figure 7. The single precision floating-point data type support is extended to other preexisting features throughout the FPGA module
Single Precision Floating-Point Data Type Development Considerations
When developing applications with single precision floating-point data type on FPGA it is paramount to consider that this data type uses more resources than the fixed-point data type, and requires more clock cycles to complete an operation. While the fixed-point data type is very efficient for hardware-based designs when it comes to speed and resource utilization, it does not provide the flexibility that the floating-point data type offers. This turns especially important when designing large applications with specific timing requirements and limited resources. The use of floating-point data type on FPGA is only recommended for applications in which the use of resources and timing is not a concern.
For applications with strict timing requirements, designers can still program advanced algorithms on FPGA using the IP Integration Node and the Xilinx Core Generator IP Palette within a Single Cycle Timed-Loop (SCTL). This allows keeping timing requirements at the same time developers take advantage of floating-point operations. It is important to note that while the floating-point data type offers many benefits, it has limited support when used in Single-Cycle Timed Loops, and uses significantly more FPGA resources than the fixed-point data type for certain operations. The following features are supported in the Single Cycle Timed-Loop with single precision floating-point data type:
- IP Integration Node
- Xilinx Core Generator IP
- Memory Items
- FIFOs
- Registers
- Local and Global Variables
Additionally, currently LabVIEW FPGA 2012 does not support subnormal numbers (denormalized numbers). A subnormal number is any non-zero number which is smaller than the smallest normal number. For instance, if a floating-point divide function is used to divide 2 numbers and its result is an extremely small number with mantissa smaller than 1, the result can be expressed as a subnormal number. The Xilinx Floating-Point Divide function treats this result as a zero with a sign taken from the subnormal number.
Mixing Fixed-Point and Floating-Point Data Types
Considering the resource consumption of floating-point operations, in some applications might be useful to mix fixed-point with floating-point operators. That is, if the inputs of our processes are already fixed-point numbers, it becomes natural to perform basic operations in this format. However, when more advanced operations appear in the algorithm it is advisable to switch to a floating-point implementation. This is the case of the implementation of a multiplier-accumulator unit (MAC) on an FPGA which is a basic building block of DSP applications.
Figure 8. Iterative accumulation algorithms are susceptible to overflow and precision errors due to data types
The multiply-accumulate operation is a common step that computes the product of two numbers and adds the product to an accumulator. When implemented in fixed-point, the FPGA design benefits from the superior speed this data type offers as well as from the minimum amount of hardware resources it demands. However, when increasing the size of the algorithm and the number of iterations that the MAC unit must process, we can run into the problem of overflowing the fixed-point number. On the other hand, floating point based MAC units lack of this problem due to the intrinsic wide dynamic range of this data type; nevertheless, its implementation can be resource expensive and slower. Thus, there is a tradeoff between data type representation capacity, speed, and space. Mixing both data types in the same algorithm will result in a reduction of FPGA’s resources consumption eliminating this way the chance of having overflowing errors.
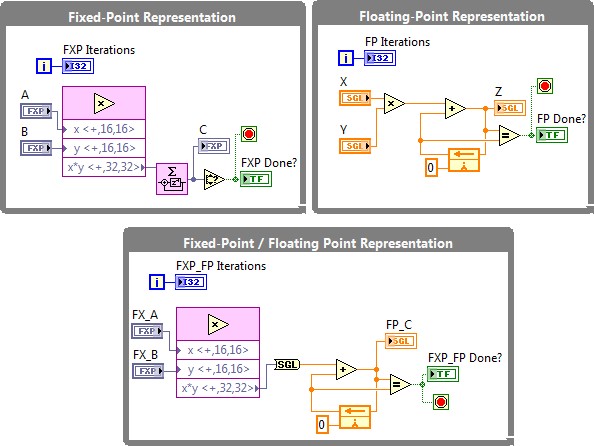
Figure 9. The multiply-accumulate operation can benefit from a mixed fixed-point / floating-point implementation in terms of dynamic range and resource utilization
The block diagram above demonstrates three different ways of implementing a simple multiplier-accumulator algorithm in an FPGA. The algorithm multiplies 2 numbers and iteratively adds them in an accumulator until it reaches a saturation status due to data type limitations. The loop with best performance is the fixed-point implementation, despite the fact it saturates fast over time. The floating-point implementation lacks of this problem dramatically outrunning fixed-point due to its high dynamic range precision; still, this implementation represents a high cost in resource consumption. Mixing both data types can lead to more balanced FPGA designs meeting specific performance requirements. While floating-point algorithms can be executed directly on FPGA, mixed implementations offer increased flexibility and superior performance in key calculations within an algorithm.
Figure 10. Mixing fixed-point and floating-point data types reduces hardware resource consumption improving performance for advanced algorithms
Benchmarking Fixed-Point and Floating-Point Data Types
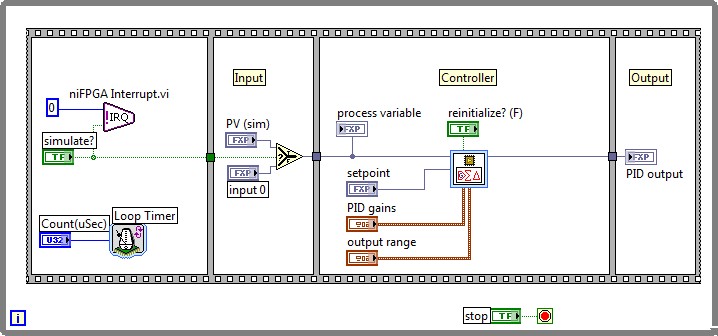
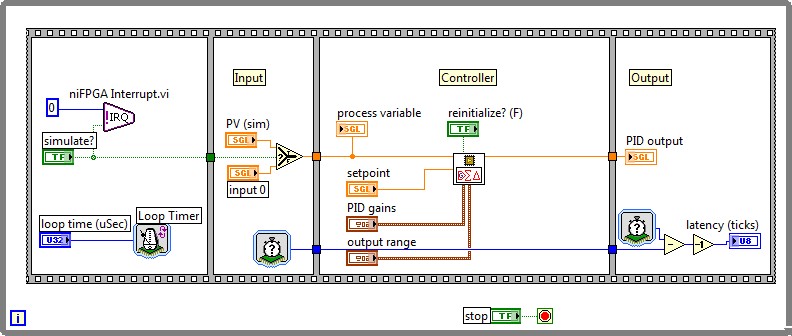
Performance, resource consumption, code reuse, algorithm complexity, and compatibility of functions are the main factors to consider when deciding where to use a specific data type within an FPGA code. This section presents a benchmarking based on the PID algorithm included in the Control palette of the LabVIEW FPGA 2012 Module. Device utilization and timing capabilities are analyzed for two PID implementations based on fixed-point and single precision floating-point. This study uses default compilation settings for the Xilinx 13.4 compilation tool. Fixed-point and floating-point PID algorithms were implemented on a NI PXI-7854R target with a Virtex-5 LX110 FPGA to serve this benchmarking. For more detailed information about the VIs used please refer to the download section.
Figure 11. LabVIEW FPGA PID control fixed-point implementation
Figure 12. LabVIEW FPGA PID control floating-point implementation
Device utilization map and final timing performance were used as comparison parameters for both implementations. As expected, single precision floating-point implementation significantly increases the amount of resources needed for the PID design; however, it leverages more accuracy and flexibility due to the 24-bit significand and increased dynamic range. Moreover, the floating-point implementation presents a higher latency, but still PID loops rates close to 800kS/s can be achieved. This way, custom sophisticated algorithms completely programmed in floating-point can be used directly in an FPGA overcoming the limitations of fixed-point implementations. For instance, in this PID example, the floating-point implementation is not limited by the 16 bit width PID output or the PID gains restriction to <±,16,8> bit of the fixed-point representation.
Device Utilization (Map) | Total | Used | Percent | ||
NI PXI-7854R | FXP | FP | FXP | FP | |
| Total Slices | 17280 | 760 | 2585 | 4.4 | 15 |
| Slice Registers | 69120 | 1418 | 4162 | 2.1 | 6 |
| Slice LUTs | 69120 | 1510 | 6275 | 2.2 | 9.1 |
| DSP48s | 64 | 3 | 3 | 4.7 | 4.7 |
Table 1. Device utilization for NI PXI-7854R benchmarking
Timing (Place and Routing) | Requested (MHz) | Maximum (MHz) | |
NI PXI-7854R | FXP | FP | |
| 40 MHz Onboard Clock | 40 | 78.20 | 110.62 |
Table 2. Timing performance for NI PXI-7854R benchmarking
Conclusion
LabVIEW FPGA 2012 offers an easy to use programming environment to inexperienced FPGA developers through familiar floating-point functions. Moreover, it empowers signal processing experts with high level tools to reduce the design time and rapidly test algorithms on FPGA. The floating-point data type support on LabVIEW FPGA 2012 opens a wide range of application possibilities while catching up with the latest technologies in the embedded systems market. LabVIEW FPGA floating-point support empowers embedded developers to:
- Reuse custom algorithms directly on FPGA without having to adapt them to FXP functions (e.g., custom control algorithms, rendering, vector graphics, anti aliasing filters, and audio algorithms)
- Implement algorithms that require a wider dynamic range than what FXP offers (e.g., accumulator functions, linear algebra DSP algorithms, etc.)
- Improve target-host DMA transfers (e.g., send analog data from FPGA to Real-Time for further processing)
It is important to note that while the floating-point data type offers many benefits, it has limited support when used in Single-Cycle Timed Loops, and uses significantly more FPGA resources than the fixed-point data type for certain operations. For more information on the functions and structures that support the floating-point data type, see the LabVIEW FPGA 2012 Help document.