Improving PID Controller Performance
Overview
Contents
- Introduction
- 1. Increased Loop Rate
- 2. Gain Scheduling
- 3. Adaptive PID
- 4. Analytical PID
- 5. Optimal Controllers
- 6. Model Predictive Control
- 7. Hierarchical Controllers
- Conclusion
Introduction
PID controllers have some drawbacks that limit their effectiveness. To start with, they work best with systems that have only one input and output (single input, single output − SISO). With these systems, you have only one variable to control and only one actuation to apply. You also can control systems that have more inputs/outputs with PID controllers if you apply decoupling techniques to the different variables so the final overall control involves a number of SISO PID controllers. Although possible, this technique is not easily implemented because it depends heavily on how tight the correlation between the variables is.
Another challenge for PID controllers (and for every control algorithm) is that the plant you need to control might not behave in a linear fashion. In other words, the output for a given input does not exhibit a linear response. Some examples of nonlinearity are dead zones, saturations, and hysteresis. Another challenge is that plant dynamics might also change over time. This can happen due to changes on the plant loads, normal wear and tear, or mechanical effectiveness in mechanical elements. To compensate for plant behavior changing over time, you need expert users to recalibrate your PID gains, which drives up costs for both labor and downtime.
Lastly, when tuning PID controllers, you might not achieve optimal overall system performance because stability is a concern, and tuning for better performance might lead to losing control over the system.
This paper examines several techniques to improve system performance and PID behavior.
1. Increased Loop Rate
One of the first options to improve the performance of your PID controllers is to increase the loop rate at which they perform. This is now possible thanks to advances in computer technology. With current technology, you can run PID loops up to 20 kHz using NI Compact FieldPoint controllers, 40 kHz with NI PXI technology, and up to 1 MHz with NI CompactRIO hardware when using PID functions based on field-programmable gate arrays (FPGAs). You can find an FPGA-ready version of the NI LabVIEW PID Control Toolkit in the LabVIEW Real-Time Module.
2. Gain Scheduling
To help cope with a system that exhibits high nonlinear behavior, you can use an advanced instance of a PID algorithm. "Advanced" means that you can select a different set of PID gains depending on the range of the operation in a particular moment. One drawback with this technique is that PID gain tuning is required for the different operating ranges. Another possible complication using gain scheduling is that range transition might lead to instabilities if the PID controller is not designed to make smooth transitions. But gain scheduling also requires tuning for each operating range. You can implement bumpless transition in the advanced version of the PID algorithm included in the LabVIEW PID Control Toolkit.
3. Adaptive PID
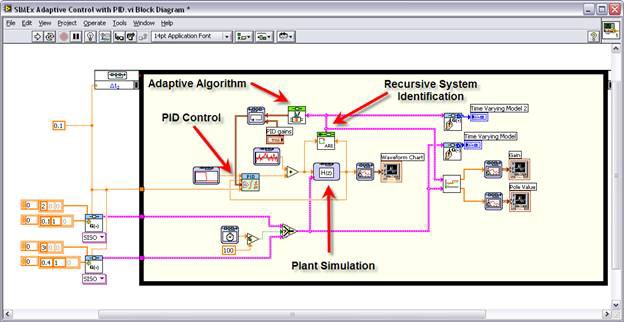
To further extend PID performance on systems that change over time, you can use another advanced variant of PID controllers that involves gains change, depending on the dynamics of your system. While gain scheduling works only with the plant output to define the operating range, adaptive PID considers both inputs and outputs to find the gains. Figure 1 shows an example of an adaptive PID implementation running in LabVIEW, where the LabVIEW PID Control and LabVIEW System Identification toolkits are combined to generate the adaptive algorithm.
Figure 1. In this example of an adaptive PID implementation running in LabVIEW, the LabVIEW PID Control and LabVIEW System Identification toolkits are combined to generate the adaptive algorithm.
4. Analytical PID
One of the current difficulties with PID controllers is the gain tuning. Although there are autotuning algorithms available, oftentimes an experienced operator is still required to fine-tune the controllers and ensure the system is stable. By using Analytical PID functionality, you can design your PID gains. You can find the right gains before putting the controller to work.
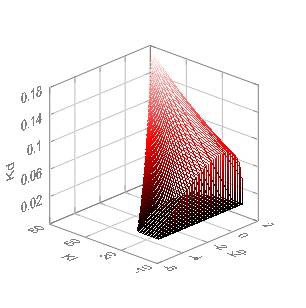
Finding the proper values for PID controller gains is a process known as tuning the controller. Typically an ad-hoc process, PID tuning involves trial and error. With the Analytical PID libraries included in the LabVIEW Control, Design, and Simulation Module (now included in LabVIEW Professional edition), you have the tools to find sets of PID gain values automatically for a given user model, which ensures system closed-loop stability. You can also input minimum gain and phase margin values to specify the optional performance constraints on the PID controller.
Figure 2. Set of Stable Gains for a PID Controller
5. Optimal Controllers
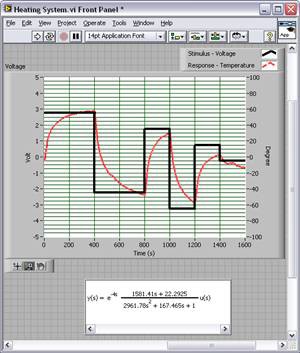
Linear quadratic controllers are designed for optimal performance on the system based on design specification. They typically require you to control a model of the system so that control gains are calculated based on a cost algorithm. This cost is user-defined and can include time to reach stable output, amount of energy used, and so on. One of the main challenges of applying optimal controllers is finding a software model of the system. Fortunately, there are tools like the LabVIEW System Identification Toolkit that identify dynamic system models directly from real-world stimulus and response signals.
Figure 3. System Identification Applied to a Heater System
6. Model Predictive Control
Traditional feedback controllers adjust control action in response to a change in the output setpoint of the plant. Model predictive control (MPC), also included in the LabVIEW Control, Design, and Simulation Module (now included in LabVIEW Professional edition), is a technique that engineers use to construct controllers that can adjust the control action before a change in the output setpoint actually occurs. This predictive ability, when combined with traditional feedback operation, enables a controller to make adjustments that are smoother and closer to the optimal control action values.
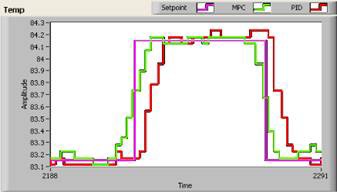
Figure 4. Comparison of an MPC Controller with a PID Controller Running on Two Temperature Chambers
Figure 4 shows a comparison of an MPC controller with a PID controller running on two temperature chambers. As you can see, the more advanced control system can better track changes on the setpoint because it has knowledge on how the setpoint is going to change and how the system reacts to a given change in the control variable.
7. Hierarchical Controllers
The aforementioned techniques are not mutually exclusive. You can combine current PID control with high-level optimal controllers like MPC or linear-quadratic regulator (LQR). These controllers, called hierarchical controllers, benefit from the use of high-level algorithms when working with nonlinearities and multiple inputs and outputs. This offers a set of smaller, easier-to-handle control problems that PID algorithms can address.
Conclusion
PID control algorithms are popular and offer many benefits such ease of use, new development help to implement other PID controller variants, and control for common industry applications. This paper examined some PID implementations and how to improve system performance when replacing current PID controllers with other advanced algorithms, either based on PID or on the dynamics of the system.
The LabVIEW PID Toolkit, System Identification Toolkit, and all VIs and functions from the Control Design and Simulation Module are now included in LabVIEW Professional, making LabVIEW Professional a powerful tool for PID control and design.