NI does not actively maintain this document.
This content provides support for older products and technology, so you may notice outdated links or obsolete information about operating systems or other relevant products.
This document provides a general programming structure for using the Measurement Studio ActiveX controls for counter applications. This structure is illustrated using Visual Basic, which facilitates the integration of ActiveX controls in an application. Because ActiveX controls are language independent, you can apply many of the concepts explained in this document to applications developed in other programming languages.
Note: Measurement Studio includes tools to build measurement applications in ANSI C, Visual C++, and Visual Basic. The Measurement Studio Visual Basic tools were formerly known as ComponentWorks.
ActiveX controls are based on the Component Object Model (COM) software architecture. COM is language and platform independent and addresses the need for code reusability and maintenance by allowing software components from different vendors to be used as parts for different applications and systems.
ActiveX controls enable software developers to encapsulate a specific functionality that can be accessed using different programming languages. Because the Measurement Studio DAQ ActiveX controls hide implementation details and provide an intuitive interface, access to DAQ hardware functionality is quick and easy.
To access the functionality of the ActiveX control, use the programming environment properties, methods, and events. Properties are variables within the ActiveX controls that you can read or write to in order to modify the behavior of the control. For example, in the CW Counter control, you can select different counter operations by setting a property.
With Measurement Studio ActiveX controls, you can set properties programmatically or by using the property pages. The property pages options allow you to quickly navigate and set control properties and to see the relation between the different properties.
Note: Property pages are available at development time only. To modify properties at run time in order to allow user interaction, you must access the properties through the code.
The following image shows the CW counter control Property Pages window.
Invoking an ActiveX control method instructs the control to perform certain action. The CW counter control provides a configure method, which instructs the ActiveX control to configure the counter hardware.
Events allow the ActiveX control to notify the application when a change occurs. When all requested measurements are taken, the CW counter fires an event, and a function within the code is called by the CW counter control. The code in this function then responds to the event (plotting the measurements acquired, for example).
Each ActiveX control has different properties, methods, and events, depending on its designated function. In order to take full advantage of the functionality of the control, you must know the properties, methods, and events it provides. For this reason, proper documentation is vital when developing applications using ActiveX controls. The extensive help files available in Measurement Studio show all properties, methods, and events of a given ActiveX control.
See Also:
ActiveX/COM Overview
A basic counter consists of a Source input pin, a Gate input pin, an Out output pin, and a count register. The following illustration shows this simple counter model.
Counters respond to output digital TTL (transistor-to-transistor logic) signals. A TTL signal is a square-pulse signal that can have a value of 0 V (logic low) or 5 V (logic high). The transition between these two stages is called an edge. The following illustration shows a TTL signal.
Signal edges are counted at the source, also known as clock signal. Depending on how the counter is configured, each active edge on the source either increases or decreases the count register. The counter gate controls when the counting occurs and can be configured for the following modes:
When in high-level mode, a low level on the gate stops the count register from increasing or decreasing, even when active edges occur on the counter source. Similarly, when in rising-edge mode, a rising edge on the gate stops the count. The count resumes with rising edge on the gate. The count register stores the number of active edges detected on the counter source. This value is used in the different measuring operations.
The following figure shows the different gating modes.
When using count, it is important to know the counter resolution (in bits) because it determines the maximum count the count register can hold. A higher resolution means a wider range in measurements and generation operations. An NI-TIO counter has a resolution of 32 bits, which means that the maximum value an NI-TIO can hold is 2^32. When the counter reaches the maximum count, it rolls over and the count starts again.
The terminal count is the pulse the counter output generates when the counter reaches maximum count. The terminal count is used in single pulse or pulse train generation operations. When you select an operation, the Measurement Studio DAQ controls perform most of the counter output configuration.
It is also important to know which counter chip you are using. E Series multifunction DAQ boards use the DAQ-STC chip, and NI 660x counter boards use the NI-TIO chip. The NI-TIO chip supports all counter operations the DAQ-STC supports, as well as some extra features that allow other counter operations, such as a start trigger, auxiliary lines, and Z Index.
Counter operations are divided into two groups: measurement and generation. All operations are controlled by two different Measurement Studio ActiveX controls. CWCounter controls measurements, and CWPulse controls generation.
The following table lists some of the operations the NI-TIO and DAQ-STC counters support.
Measurement Operations
| Generation Operations
|
| Event counting | Single pulse generation |
| Time measurement | Single triggered pulse generation |
| Period measurement | Retriggerable pulse generation |
| Frequency measurement (uses two counters) | Pulse train generation |
| Semi-period measurement | Frequency shift keying (FSK) |
| Two-signal edge-separation measurement (NI-TIO only) | |
| Position |
Measurement Operations
You can perform measurement operations in buffered or non-buffered mode. Buffered operations allow for faster consecutive measurements. Simple position measurements can be taken using the DAQ-STC counter. NI-TIO counters provide certain features that make them more suitable for position measurement, such as the Z Index channel and encoder type selection.
The method for taking measurements in buffered and non-buffered mode varies depending on the operation.
Generation Operations
The main advantage of waveform generation with counters is precise timing. Counters allow for very precise pulse width and pulse train frequency generation. You can use these signals to control and synchronize other operations, such as analog and digital I/O.
For a complete list and description of counter operations for DAQ-STC and NI-TIO counters, refer to the E Series Help and the TIO Help by selecting Start >> Programs >> National Instruments >> NI-DAQ and selecting Browse Device Documentation. These documents are also available at ni.com/manuals.
This section describes the general layout of a counter application in Visual Basic using Measurement Studio ActiveX controls. This structure applies to most counter operations. This section also describes the most common properties, methods, and events used in counter applications.
Before Getting Started
Before programming your application, you must add the Measurement Studio ActiveX controls to the Visual Basic developing environment. To add these components to your project, follow these steps:
In order to use a control in your application, you must place the control on the form. Once on the form, you can access the control’s properties and methods in the code through the control name. The default names of the counter control and pulse control are CWCounter1 and CWPulse1, respectively.
Setting Counter Properties
The counter properties specify which operation to perform and how to perform it. Properties allow you to specify parameters such as the type of operation, buffer setting, buffer size, pulse duration, and the source and gate signal source. The type of operation determines which properties to set.
Property pages allow easy navigation through the counter properties of each counter operation. Depending on the counter operation selected, the property pages automatically enable and disable properties. This feature is useful when setting counter options in your code because it allows you to see the relation between different properties. The Help button on the property pages opens the reference for the control and provides detailed explanations of control properties.
Set the counter properties through the property pages of the ActiveX control or within your code. To access the property pages, right-click the CWCounter or CWPulse icon on the form, and select Properties. The following figure shows the property pages for the CWCounter control. Refer to the Line Selection section of this tutorial for more information.
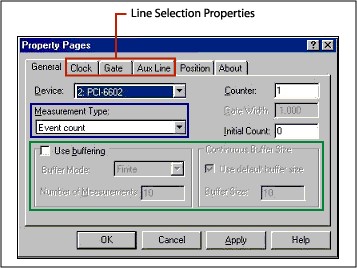 |
The red area shows the Clock, Gate, and AuxLine property pages. These pages allow you to select the signals the counter uses for each of these counter terminals. The blue area shows the Measurement Type. This drop-down list allows you to select the counter operation. The green area shows the buffer settings.
|
The following figure shows the property pages for the CWPulse control. Refer to the Line Selectionsection of this tutorial for more information.
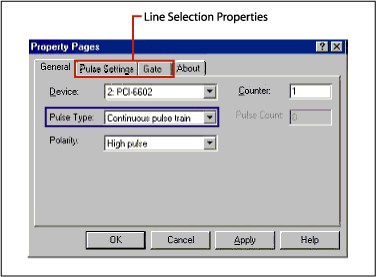 |
The red area shows the Pulse Settings and Gate property pages. These pages allow you to specify the signal the counter uses for the counter operation.The blue area shows the Pulse Type. This drop-down list allows you to select the counter operation.
|
Property pages allow you to set properties at development time that remain fixed when your application runs. All properties available on the property pages are available in the code. Properties set in the code overwrite values set on the property pages. To set properties at run time, you must explicitly set them in your code. The following figure shows how to access the properties in your code.
In Visual Basic, typing the control name followed by a period pulls up a list containing the available control properties and methods. Properties have the icon next to them, and methods have the
icon next to them. This list allows you to quickly select the desired property or method without having to contend with syntax.
Configuring the Counter
When the properties are set, you must configure the counter by calling the CWCounter1.Configure or the CWPulse1.Configure method. Calling this method programs the counter with the properties specified in the previous step but does not start counter operation.
The CWPulse control offers an additional Reconfigure method that allows you to modify only the pulse specifications in a counter generation operation. You can use this method to modify the frequency or duty cycle of a pulse train on the fly.
Starting (Arming) the Counter
When the counter is configured, start the operation by calling the CWCounter1.Start or the CWPulse1.Start method. Calling this method begins the measurements or the generation.
On finite operations, such as single-pulse generation, the Start method can be called to restart the operation. The counter remains configured until the Reset method is called or the configuration is changed using the Configure method.
The counter remains armed until it finishes the operation. After the operation is performed, the counter can be rearmed or restarted using the same configuration. In retriggerable pulse generation, the counter rearms automatically after the pulse is generated.
Getting Measurements
Note: This section applies to measurement operations only.
When the counter starts, you can get the counter measurement either by querying the counter or through an event, depending on the counter operation. By knowing how events are generated, you can determine which of these your program uses to get the counter measurements.
When the counter is ready to transfer data, the DAQ hardware generates a signal that informs the system that data needs to be transferred. When the data is transferred to the Traditional NI-DAQ (Legacy) driver, the driver uses an event to inform the application that data is ready. The application then handles the event and retrieves the data. An event is generated anytime the counter determines that the operation is complete.
For other operations, such as non-buffered event counting, time measurements, and position measurements, the program must query the counter value. When performing these operations, the counter continuously changes the count register, depending on the signals it receives. The DAQ hardware cannot detect when the operation is complete, so the application must query the counter for the measurement.
The two CWCounter methods that query the counter for the value of the count register are CWCounter1.ReadMeasurement and CWCounter1.ReadCounter. The ReadMeasurement method returns the counter measurement in the units of the measurement. The ReadCounter method returns the raw value of the counter’s count register. ReadMeasurement is the more commonly used method.
For period, semi-period, two-signal edge-separation, and frequency measurements, the counter takes a single reading and stops. In these cases, the DAQ hardware can determine that the operation is complete and then fire an event to inform the application the measurement has been taken.
In all buffered operations, the measurements are taken when an active edge occurs at the counter gate. The counter is programmed to take a predetermined number of measurements. When these measurements are taken, the counter can transfer the data to the system, and an event is fired. In buffered operations, the application uses the Callback function to handle the event. When the measurements are ready, the system automatically calls this function. The Callback function, shown below, automatically generates in your code by double-clicking the CWCounter icon on the form.
Private Sub CWCounter1_AcquiredData(Measurement As Variant, Overflow As Boolean)
Text1.Text = Measurement
End Sub
The Callback function has two parameters that the Traditional NI-DAQ (Legacy) driver provides: the Measurement parameter and the Overflow parameter. The Measurement parameter contains the data returned from the counter. It can be a single value or an array of values, depending on the requested operation. The above code returns a single value, which appears in a text box. The Overflow parameter contains a TRUE or FALSE value, which determines if there is an overflow in the count register. If the counter overflows, the measurement is invalid, and a slower frequency timebase signal should be used for this measurement.
Note: Overflow detection is not supported with buffered operations.
Stopping and Resetting the Counter
In finite operations, the counter stops when the operation finishes. In continuous operations, the counter must be explicitly stopped. For example, in a continuous pulse train generation operation, if the application configures and starts the counter but does not explicitly stop the counter, the application will finish execution and the counter will continue to generate a pulse train.
Calling the CWCounter1.Stop method stops a counter operation. When the counter is stopped, it retains its current configuration. Calling the Start method restarts the operation.
Calling the CWCounter1.Reset method resets the counter, which means that the Configure method must be called before starting a new counter operation. This means that the configure method must be called before starting a new counter operation.
This general application structure applies to all counter operations in Visual Basic using Measurement Studio ActiveX control. The next section provides more detailed explanations of other configurations and features available with the Measurement Studio ActiveX controls.
Quadrature Encoder Signals
A quadrature encoder is a sensor that measures rotational or linear position. The quadrature encoder generates two pulse trains with a phase relation of 90 degrees. These two signals are generally referred to as channel A and channel B. One pulse train leads the other depending on the direction the system being measured is moving. The following figure shows the signals in both directions.
When the system moves in Direction 1, channel A leads channel B. When the system moves in Direction 2, channel A follows channel B. The rising edge of channel A occurs on channel B’s high or low level, depending on the direction of the system. This property allows the counter to determine the direction of the movement.
To perform position measurements with a counter, connect channel A to the counter source and channel B to the counter Up/Down line. The Up/Down line senses the signal level to determine the counter’s count direction. When the system rotates in one direction, the counter counts up. When the system rotates in the opposite direction, the counter counts down.
Quadrature encoders measure relative position. Commercial quadrature encoders provide an index channel, also known as Z Index channel. This channel generates a pulse on each revolution of the encoder. NI-TIO devices use this pulse as a reference point by resetting the count register to a known value. For more information about the Z Index channel, refer to the Z Index Channel section of this document.
Note: The NI-TIO (NI 660x) user documentation specifies the pin numbers in terms of channel A, channel B, and Z Index channel.
DAQ-STC Quadrature Encoder Measurement
You can configure NI-TIO devices to perform position measurements. This operation automatically configures all lines to accept the encoder signals. Even though DAQ-STC (E Series) devices do not support this operation mode, you can perform position measurements using a DAQ-STC counter by manually setting up the lines. The main disadvantage of using a DAQ-STC device to perform a position measurement is that, because it does not support the Z Index channel, it is not possible to externally mark a reference point.
In order to measure encoder signals, you must configure the counter source to be external and enable the Up/Down line. In this setup, the counter performs simple event counting, and the external signal connected to the Up/Down line (channel B) determines the direction of the count.
The counter in DAQ-STC devices is configured for simple event counting, as shown in the following figure.
The following figure shows how to set up up an external source and enable the Up/Down line.
Note: The Up/Down lines for E Series devices are DIO 6 for counter 1 and DIO 7 for counter 2.
For more information about quadrature encoders, refer to the Using Quadrature Encoders with E Series DAQ Boards article.
Z Index Channel
Note: The Z Index channel is only supported on NI-TIO devices (NI 660x).
Commercial encoders provide a Z Index channel, which serves as a reference point in position measurements. The counter reloads its count register with a predetermined value when a high pulse on the Z Index line is received. The polarity of the pulse cannot be changed.
To set up the Z Index properties, select Position in the Measurement Type field, and click the Position tab.
This figure highlights the Z Index properties. Set the following three properties:
The reload phase specifies the state that channels A and B must be for the reload to occur. The following figure shows the four possible phases.
The timing characteristics of the Z Index channel with respect to channels A and B differ between encoder models and designs. NI-TIO devices give you the flexibility to select the reload phase to adapt to different encoder designs. The following figure illustrates the reload when the selected phase is A low and B low.
Note: The Z Index line uses the counter’s gate pin on the front terminal of the 660x boards. The 660x user documentation specifies the pin number used in terms of Z Index channel.
Line Selection
To provide flexibility, counters can use a number of different signal sources as the counter’s source and gate signals.
Before discussing the properties involved, it is important to review the terminology. A counter has two main inputs: source and gate. In addition to source and gate, NI-TIO devices provide a Z Index channel, an AuxLine, and an Up/Down line for each counter. The term source refers to the actual counter input and not to the PFI pin associated to the source input. Other signal sources can also be connected to the counter’s source input. This also applies to the gate and AuxLine. The following figure illustrates this concept for counter 1 of a NI-TIO device.
In this figure, PFI 35 is associated by default as the source for counter 1. A source selection circuit allows you to change that default setting. The signals selected can be internal or external.
Note: To avoid confusion, Measurement Studio ActiveX controls refer to the source input as the timebase.
In the CWCounter control, the Clock and Gate Property Pages allow you to select the source and gate signals. The following figures show the signal options.
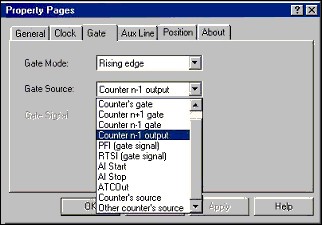 | 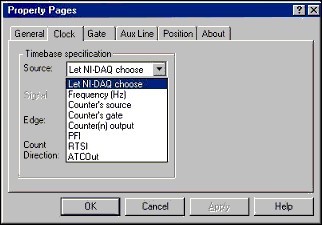 |
Most of the signal options are the same for the source and gate inputs.
Note: AuxLine selection only applies to NI-TIO devices when configured for two-edge separation measurements. The signal options are the same used for the source and gate inputs.
The following figure shows the properties available to programmatically select the signals for the Source, Gate, and AuxLine.
Note: The Z Index signal source is the default PFI gate pin for a given counter and cannot be changed. For counter 1, the Z Index signal must be connected to PFI 34.
Line Filtering
NI-TIO devices provide a simple digital filter for the PFI lines. Two clocks are involved in line filtering: an internal sampling clock (usually the maximum timebase) and a filter clock. A signal edge is transferred to the counter if the new state is maintained for at least two rising edges of the filter clock. Each rising edge of the sampling clock stores the state of the signal on the PFI pin.
The frequency of the filter clock determines the minimum pulse width required for a pulse to be considered valid. A filter clock of 100 ns blocks pulses shorter than 50ns and passes pulses longer than 100 ns. Pulses between 50 ns and 100 ns may or may not pass.
NI-TIO devices provide four filter settings: 5 us, 1 us, 500 ns, and 100 ns. Additionally, any counter output can be used as the filter clock, allowing custom frequencies. Lines can be individually configured using the following properties:
These properties are not available on the property pages. Refer to the hardware documentation and the Measurement Studio help files for more information about line filtering.
Transfer Modes: DMA vs. Interrupts
In buffered measurements, data needs to be transferred from the DAQ device to the PC memory (your application). There are two transfer modes available, interrupts and direct memory access (DMA).
In interrupt mode, the DAQ device generates an interrupt, which means that it signals the CPU that it needs to transfer data. When the CPU receives the interrupt signal, it calls an interrupt handler. The interrupt handler finds the device that needs attention and then proceeds to transfer the data from the DAQ device into system memory.
In DMA mode, the DAQ device requests control of the PCI bus and transfers the data directly to system memory without CPU intervention. Of the two modes, DMA mode allows for faster data transfer rates because it requires less overhead. The drawback is that DMA channels are a limited resource. A DMA channel is the system resource that allows to the DAQ device to request control of the PCI bus. In the same way, an interrupt line is the system resource that allows the DAQ device to interrupt the CPU to request a data transfer operation.
Each counter occupies either an interrupt line or a DMA channel. For example, a PCI-6602 counter board has three DMA channels and five interrupts available. This means that only three counters can use DMA transfer mode. If any other counter is used, it must use an interrupt line.
The transfer mode of a counter can be specified using a method in the CWDAQTools ActiveX control. The methods exported by this control provide additional functionality, such as calibration, and operations that affect the DAQ device. From this control, the SetDAQDeviceInfo method allows you to specify the transfer mode for counter in your board. Refer to the Measurement Studio help file for detailed information about the parameter used by this method.
Note: Refer to the hardware documentation for transfer rate benchmarks for interrupt and DMA modes.
Start Trigger
Counters are armed using the start method. Since the calls to the driver are done sequentially, counter are armed in sequence. To allow simultaneous arming of counters, NI-TIO devices provide a Start trigger signal, which is not the same trigger signal used in triggered pulse generation. The start trigger signal applies to all counters and for both measurement and generation operations. When the trigger signal is received the counters are armed. The following figure shows the property used to enable the start trigger.
Selecting HardwareTrigger enables the start trigger. Use the DAQTools ActiveX control to select the signal source. This property is not available in the property pages. Refer to the Measurement Studio help files for more information about how to configure the start trigger.