Benefits of Deep Memory in High-Speed Digitizers
Overview
· Signal modulation analysis
· Jitter performance characterization
· Pulse height measurements
· Video signal tests
As always, measurement system power is key to characterizing product performance, analyzing system response, and detecting defects. National Instruments high-speed digitizers deliver improved time and frequency measurements with their deep onboard memory options.
Time-Domain Benefits
When doing time-domain analysis, it is important to know the maximum time for which you can acquire data using a given sample period or sampling rate. Because data is ultimately transferred from the digitizer to host computer memory for storage, display, and further analysis, digitizer data transfer speed is limited by the data bus, such as PCI. Deep memory is necessary because oftentimes the data bus does not have the bandwidth to keep up with the full sampling rate of high-speed digitizers. With deep memory, the digitizer can sample at its maximum rate, store data locally, and then transfer the data to the host computer once acquisition is complete. Digitizers with deep memory can maintain their maximum sampling rate for longer periods of time, so their acquisition time window is increased. The acquisition time window determines whether you will be able to acquire the entire signal needed to perform your analysis. You can calculate your acquisition time window using the following equations (S/s = samples/second):
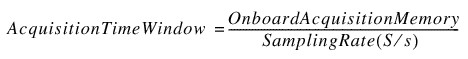
Or in terms of maximum sampling rate (limited by digitizer specifications):
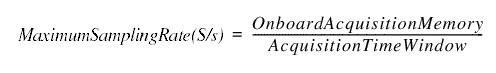
*Onboard acquisition memory = maximum number of samples that can fit in onboard memory of the digitizer
When selecting the sampling rate you must take the Nyquist theorem into consideration. The Nyquist theorem states that a signal must be sampled at a rate at least twice its highest expected frequency component in order to accurately reconstruct the waveform. A sampling rate below the Nyquist level results in aliasing of the high-frequency content inside the spectrum of interest. An alias is a false lower frequency component that appears in data acquired at too low a sampling rate. Figure 1 depicts a 25 MHz sine wave acquired by a 30 MS/s ADC. The dotted line represents the 25 MHz frequency aliasing back in the passband, falsely appearing as a 5 MHz sine wave. In order to avoid aliasing, you must sample this 25 MHz sine wave at a rate greater than 50 MHz (MS/s). This is just one example of the importance of maintaining high sampling rates during your signal acquisition.
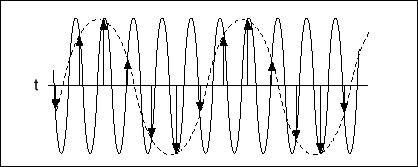
Figure 1. Aliasing
In the previous equations, you can trade off sampling rate for a longer acquisition time window, because the amount of digitizer onboard acquisition memory is fixed. Deep onboard acquisition memory gives you the ability to capture data over long time periods while maintaining high sampling rates. On digitizers with limited memory, it is especially difficult to capture packetized waveforms such as video, disk drive read channel, and serial communication signals made up of multiple components with relatively long time periods. Oftentimes, the only way to acquire the entire signal envelope is to lower the sampling rate. However, a slower sampling rate results in degradation of signal detail and can cause aliasing on individual high-speed components within the signal envelope. For example, a NTSC video signal has a frame rate of 30 frames per sec (fps) and contains frequency components from 30 Hz to 4.2 MHz. To capture an entire frame at 100 MS/s would require a digitizer to acquire more than 3.3 MB (3.3 milllion samples) of data. A digitizer with a 1 MB memory would have to reduce its sampling to around 30 MS/s or less. Figures 2 and 3 illustrate the results of signal degradation when reducing the sampling rate from 100 to 20 MS/s when capturing an entire frame of a NTSC video signal. Notice the loss of signal information in the color burst region of the horizontal line.
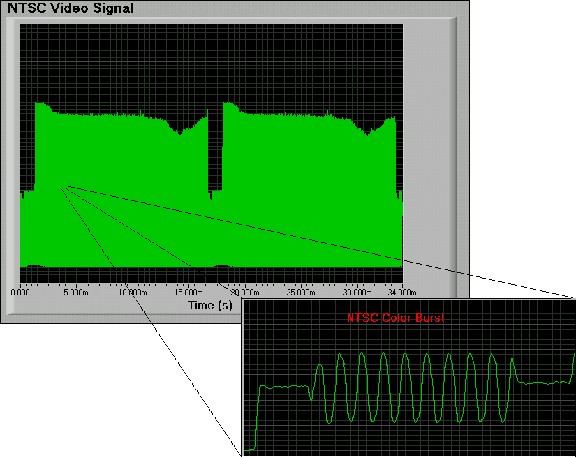
Figure 2. Single Frame of NTSC video sampled at 100 MS/s
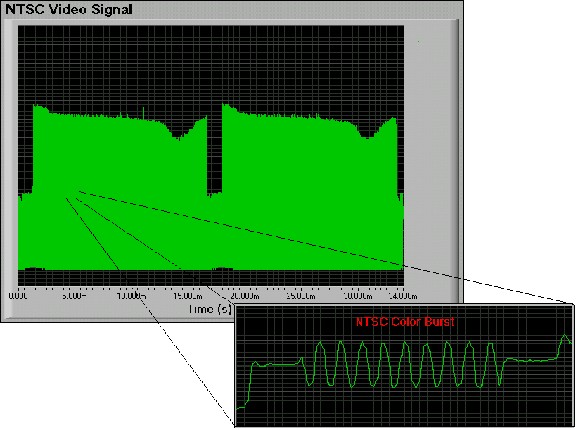
Figure 3. Single Frame of NTSC video sampled at 20 MS/s
Figure 4 illustrates the benefits of using deep onboard memory to maintain high sampling rates over an extended acquisition time window. A digitizer with 100 MS/s sampling rate and 100 KB of onboard memory can sustain its maximum sampling rate for only 1 ms. To acquire data for 2 ms this digitizer would have to decrease its sampling rate to 50 MS/s or less. A digitizer with 100 MS/s sampling rate and 32 MB of onboard memory can sustain its maximum sampling rate for up to 320 ms.
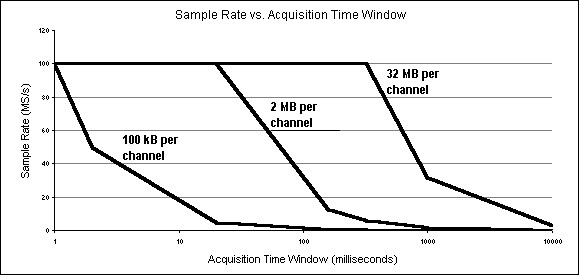
Figure 4. Sample Rate vs. Acquisition Time Window With Various Memory Options
A National Instruments NI 5112 high-speed digitizer can also be integrated with the NI 5411 arbitrary waveform generator to capture and regenerate waveforms for an extended length of time, simplifying the creation of complex signals for manufacturing test applications. For these applications, one solution is to capture a “gold” standard signal with the NI 5112 high-speed digitizer and later output that signal with the NI 5411 arbitrary waveform generator. For instance, video signals captured with the NI 5112 high-speed digitizer can be regenerated on the NI 5411 or NI 5431 to test video equipment such as television and DVD devices. In addition, the NI 5112 can synchronize with the NI 5411 to perform stimulus-response measurements over long periods of time. The NI 5112 and the NI 5411 phase-lock to the same reference clock source, ensuring the precise timebase alignment required for these applications.This advanced timing and triggering integration is inherent to the versatile PXI architecture and can be implemented on PCI via the RTSI bus.
Frequency-Domain Benefits
High-speed digitizers are commonly used to acquire signals for frequency-domain analysis. When taking frequency-domain measurements, it is important to consider the effects of aliasing. Again, the Nyquist theorem states that you must sample at a rate twice the maximum frequency of the acquired signal, otherwise high-frequency signal components may alias and appear as low-frequency signals in the passband. If your sampling rate is greater than twice the highest frequency of the acquired analog signal, then your frequency analysis will be valid.
Frequency Resolution
There are several FFT algorithms used to compute the Discrete Fourier Transform (DFT). The NI-SCOPE instrument driver for high-speed digitizers uses the split-radix real FFT algorithm. The split-radix algorithm is calculated on n points, where n is a power of 2. If the number of acquired points is not a power of 2, zeros are padded at the end of the waveform to increase the number of points to the next higher power of 2. Although padding increases the number of points, it does not affect the FFT results. Performing an FFT on n points in the time domain yields n/2 points in the positive frequency domain. These points define a range of frequencies between DC and half your sampling rate. Once the number of points is known, you can compute the frequency resolution of your FFT measurement using the following formula:
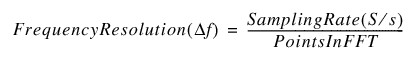
Per the above equation, frequency resolution improves as sampling rates decrease and points acquired increase. Decreasing the sampling rate is often an undesirable way to increase resolution because it decreases the frequency span, or usable bandwidth. With deep onboard acquisition memory, the digitizer can maintain a high sampling rate for a long period of time, effectively increasing the number of points acquired and therefore improving frequency resolution.
For example, using a digitizer with 100 KB of memory and 100 MS/s maximum sampling rate, we can compute the frequency resolution from the equation above. At a sampling rate of 100 MS/s and the number of samples set to 100,000 the frequency resolution is 762.9 Hz and the frequency span is DC to 50 MHz. The 100,000 points will be zero-padded to 131,072 points and 100 MS/s divided by 131,072 yields a frequency resolution of 762.9 Hz. Using the NI PCI-5911 Flex ADC high-speed digitizer with 16 MB of onboard memory, you can achieve a frequency resolution of 5.96 Hz at 100 MS/s with the same frequency span of DC to 50 MHz.
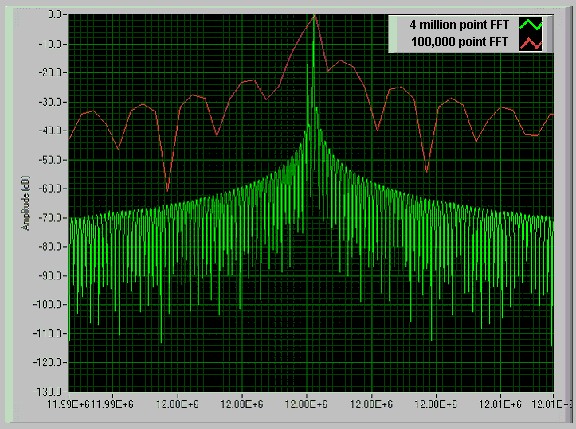
Figure 5 demonstrates the importance of optimized frequency resolution when performing frequency analysis on an acquired waveform. Two signals closely spaced in frequency appear as one peak in an FFT analysis with limited frequency resolution. The acquired signal in Figure 5 contains 12.000000 MHz and 12.000180 MHz frequency components. A digitizer with 100 KB of memory and 100 MS/s maximum sampling rate cannot resolve these two frequencies. Even lowering the sampling rate to exactly twice the signal bandwidth would not enable the instrument to resolve the two signals. You can resolve these two peaks with the use of a digitizer with deep onboard memory by acquiring 4 million samples.
Figure 5. FFT Frequency Resolution When Acquiring 4 Million Points vs. 100 Thousand Points
Spectral Leakage and Windowing
When you use the Discrete Fourier Transform (DFT) or FFT to find the frequency content of a signal, it is assumed that you have acquired a periodically repeating waveform. This is because the FFT tries to approximate the Continuous Fourier Transform (CFT) by replicating the finite acquisition an infinite number of times. If the acquired data does not contain an integer number of periods, then the infinite sequence will have discontinuities between adjacent finite acquisitions. Figure 6 illustrates the effects of acquiring a noninteger number of periods.
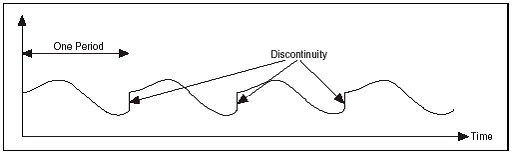
Figure 6. Discontinuities Caused by Replicating a Finite Acquisition with Noninteger Periods
These artificial discontinuities show up in the FFT spectrum as high-frequency components not present in the original signal. These frequencies can be much higher than the Nyquist frequency and will be aliased between 0 and fs/2, where fs is your sampling rate. The spectrum you get by using a FFT, therefore, is not the actual spectrum of the original signal, but a "smeared" version. It appears as if energy at one frequency leaks into other frequencies. This phenomenon is known as spectral leakage. Spectral leakage causes the fine spectral lines to spread into wider signals.
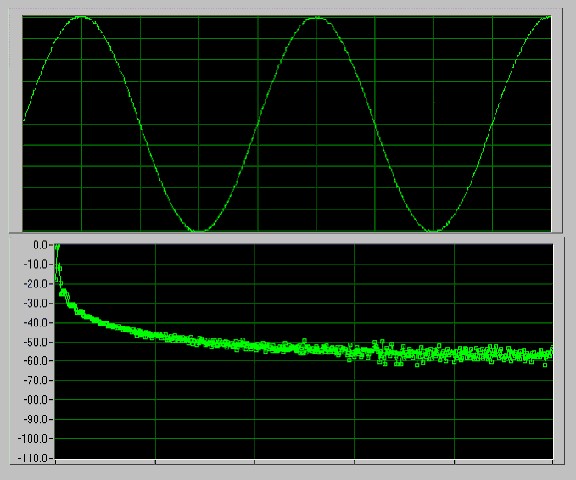
Figure 7 below illustrates a sine wave, sampled from a NI PCI-5911 digitizer, and its corresponding FFT amplitude spectrum in decibels. The time-domain waveform has an integer number of cycles (2 in this case), so the assumption of periodicity does not create discontinuities.
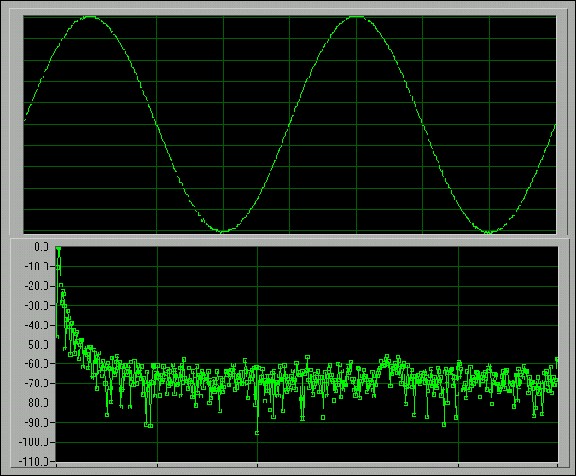
Figure 7. FFT Spectrum without Spectral Leakage
Figure 8 is a spectral representation of sampling a noninteger number of cycles of the time-domain waveform. The periodic extension of this signal creates a discontinuity similar to periodic extension shown in Figure 6. Notice how the energy is spread over a wide range of frequencies, so the relative height difference between the FFT peak amplitude and the neighboring bins is reduced. This "smearing" of the energy is called spectral leakage. Spectral leakage distorts the measurement in such a way that energy from a given frequency component is spread over adjacent frequency bins.
Figure 8. FFT Spectrum with Spectral Leakage
Spectral leakage exists because the noninteger number of periods in the signal acquired creates discontinuities between adjacent portions of the infinite sequence. You can minimize the effects of performing an FFT over a noninteger number of cycles by using a technique called windowing. Windowing reduces the amplitude of the discontinuities at the boundaries of each finite sequence acquired by the digitizer.
Windowing consists of multiplying the time record by a finite-length window with an amplitude that varies smoothly and gradually towards zero at the edges. Therefore, when performing an FFT spectral analysis on a finite length of data, you can use windowing to minimize the transition edges and thus eliminate the discontinuities in the infinite sequence. The NI-SCOPE instrument driver for high-speed digitizers provides six choices for windowing functions including rectangular, Hanning, Hamming, Blackman, triangle, and flat top.
Figure 9 illustrates the benefits of using the Hanning window when acquiring a noninteger number of periods is your signal. The first graph shows the original signal acquired from Figure 8. The second graph shows the time-domain signal after the Hanning window has been applied. The third graph shows the FFT spectrum of the windowed signal. Notice the dramatic decline in spectral leakage in the windowed FFT in Figure 9 as compared with the nonwindowed FFT of the same signal in Figure 8.
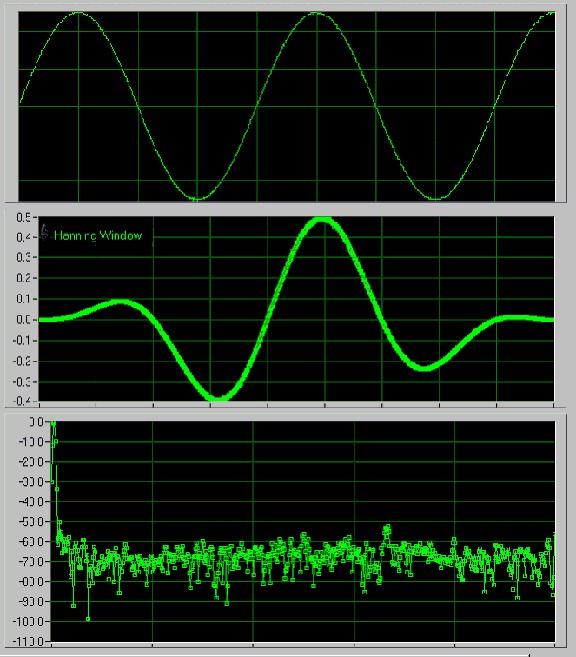
Figure 9. Hanning Windowed FFT Spectrum
If the waveform of interest contains two or more signals slightly diifferent in frequency, spectral resolution is important. In this case, it is best to choose a window with a very narrow main lobe such as the Hanning window. If the amplitude accuracy of a single frequency component is more important than the exact location of the component in a given frequency bin, choose a window with a wide main lobe such as the flat top window. Hanning is the most commonly used window type because it offers good frequency resolution and reduced spectral leakage. However, considering the increased frequency resolution offered by digitizers with deep memory, the flat top window offers some benefit over the Hanning window. The flat top window offers the best amplitude accuracy and the sharpest side lobe fall off. Visit National Instruments Developer Zone for more information on windowing and windowing techniques.
Dynamic Range
When taking frequency-domain measurements it is important to know the dynamic range of your measurement system. The dynamic range is the ratio of the highest signal level to the lowest signal level that your measurement system can handle. This tells you the smallest signal amplitude that can be measured in the presence of a larger amplitude signal.
Internal imperfections in the analog-to-digital converter (ADC) limit the dynamic range of a digital oscilloscope. Also, nonlinear responses in the analog front end and the ADC cause harmonic distortion that shows up as artifacts in the FFT spectrum analysis.
Figure 10 shows an FFT spectrum of a 10 MHz signal acquired with a National Instruments PCI-5911 high-speed digitizer. Note that the additional spectral lines that appear on the graph are not part of the original 10 MHz signal. The dynamic range between the fundamental 10 MHz signal and the largest spectral artifact at 30 MHz is about 46 dB.
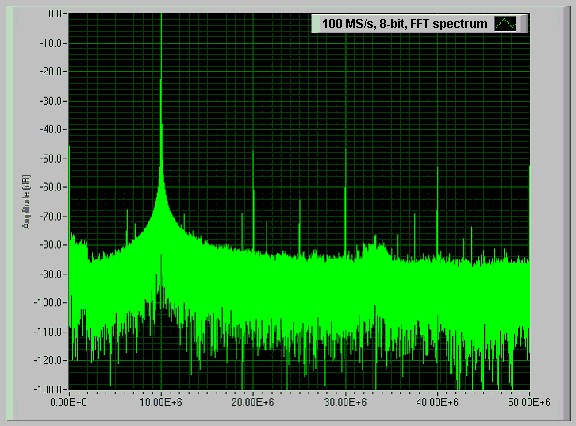
Figure 10. FFT Spectrum on a 10 MHz Signal at 100 MS/s
Reducing the asynchronous noise floor can be accomplished by increasing the number of samples used to calculate the FFT spectrum. Each FFT bin shows all the energy in that bin. Taking more samples for an FFT narrows the bandwidth of each bin, which in turn increases the frequency resolution of your FFT spectrum. Narrowing the bandwidth of each bin lowers the total noise in each bin, and reduces the noise floor. This improvement in the noise floor is realized because increasing the number of points in the FFT calculation does not change the total noise power of the entire FFT spectrum. Figure 11 demonstrates the effect of increasing the number of points acquired from 1024 points to 4 million.
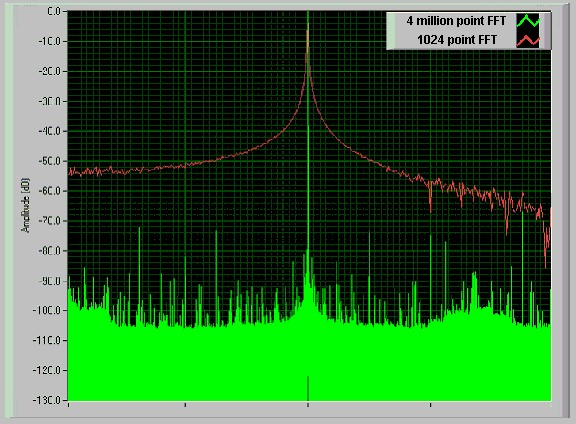
Figure 11. FFT Spectrum With 4 Million Points vs. 1024 Points
Increasing the number of samples reduces the noise floor from asynchronous noise sources, and reveals additional spectral lines that occur because of internal imperfections of the digitizer. Some digitizers include specifications for effective number of bits (ENOB) or signal-to-noise ratio (SNR). SNR is the ratio of total signal power to noise power, usually expressed in decibels (dB). SNR and ENOB can be calculated using the following formulas:

The PCI-5911 high-speed digitizer features patented Flex ADC technology, which delivers increased ADC resolution and increased dynamic performance at lower sampling rates. For example, the PCI-5911 has an effective resolution of 11 bits when sampling at 12.5 MS/s and 19.5 bits when sampling at 50 kS/s. The unique technology of the Flex ADC delivers a variety of resolution options over a large range of sampling rates. Figure 12 shows the gain in dynamic range when lowering the sampling rate to 5 MS/s at a typical effective resolution of 14 bits. The dynamic range increases to around 83 dB.
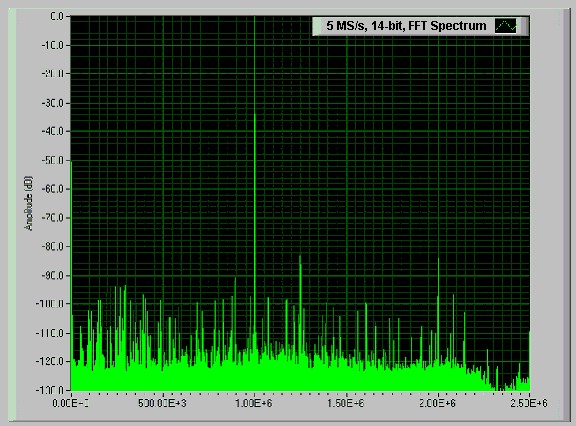
Figure 12. FFT Spectrum with NI PCI-5911 Flex Resolution at 5 MS/s and 14 bit effective resolution
Averaging
You can perform two types of averaging on data acquired by a digitizer. Time-domain averaging, also known as waveform averaging, is performed on the time-domain signal before computing the FFT. FFT averaging, by contrast, is performed by acquiring each waveform, computing the FFT, and then averaging the FFT spectra. Each type of averaging offers unique benefits.
Time-domain averaging is computed by averaging waveform data acquired from multiple triggers. This attenuates the effects of internal, asynchronous noise effects from the digitizer, thus increasing dynamic range. The noise floor is reduced to an extent directly related to the number of averages, but the variation in the noise floor remains constant. These effects are illustrated in Figure 13, which shows the benefits of waveform averaging on the dynamic range of an acquired signal.
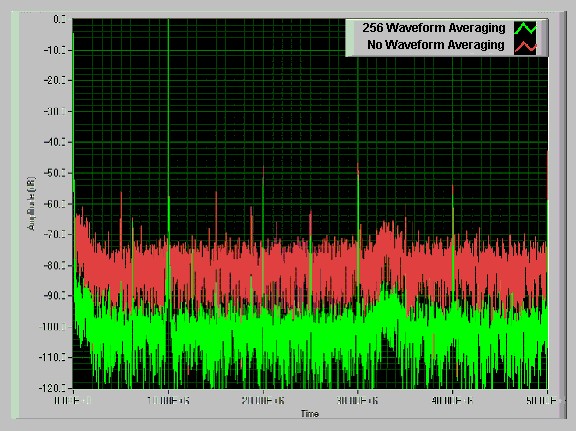
Figure 13. Waveform Averaging Spectrum
FFT averaging is computed by acquiring each waveform, computing the FFT, and then averaging the FFT spectra. This type of averaging is useful for reducing variation in the noise floor. Figure 14 illustrates the effect of FFT averaging.
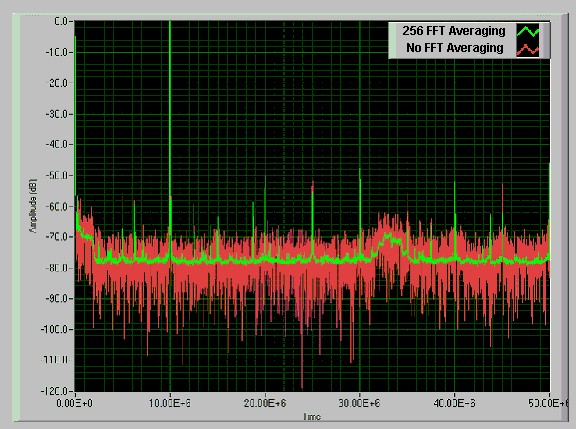
Figure 14. FFT Averaging Spectrum