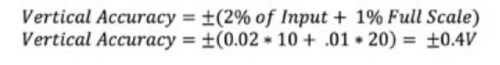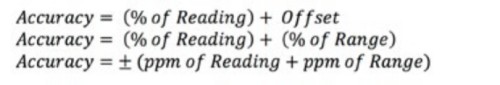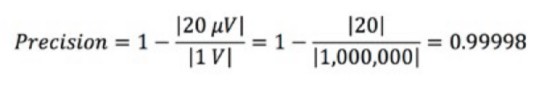アナログサンプル品質:確度、感度、精度、ノイズ
概要
測定サンプルの品質を理解し、改善するために、感度、確度、精度、ノイズについて学びます。
内容
測定感度
サンプルの品質を参照する際は、測定の確度と精度を評価する必要があります。ただし、最初にオシロスコープの感度を理解することが重要です。感度とは、測定デバイスが応答する原因となる可能性のある入力信号の最小変化です。言い換えれば、入力信号が一定量 (つまり一定の感度) 変化すると、デジタルデータの変化を確認できます。
感度を分解能やコード幅と混同しないでください。分解能はコード幅を定義します。これは、計測器が値を表示する離散レベルです。しかし、感度は計測器が値の変化を記録するために必要な電圧の変化を定義します。たとえば、測定範囲が10 Vの計測器は1 mVの分解能で信号を検出できますが、検出可能な最小電圧は15 mVの可能性があります。この場合、計測器の分解能は1 mVですが、感度は15 mVです。
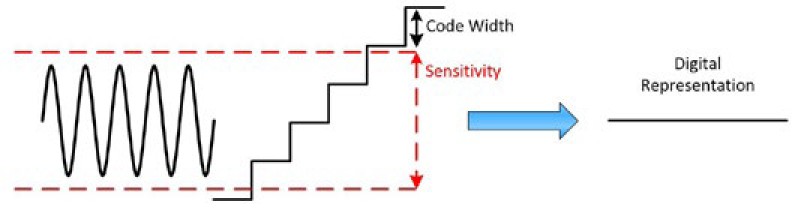
場合によっては、感度がコード幅よりも大きいことがあります。一見すると、これは直感に反するように思われるかもしれません。これは、電圧が表示可能な量だけ変化しても、登録できないという意味ですか。はい。この利点を理解するには、一定のDC電圧を考えてみましょう。電圧が偏差なく、正確に一定であれば素晴らしいのですが、図1に示すように、信号には常にわずかな変動があります。感度は赤い線で示され、コード幅も同様に示されています。この例では、電圧は感度レベルを超えることはないため、コード幅よりも大きい場合でも、同じデジタル値で表されます。これは、ノイズを拾わず、信号を定電圧としてより正確に表すという利点があります。
図1:コード幅よりも大きい感度は、ノイズの多い信号の平滑化に役立つ。
信号が実際に立ち上がり始めると、感度レベルを超え、異なるデジタル値で表されます。図2をご覧ください。測定が感度よりも正確になることはあり得ません。
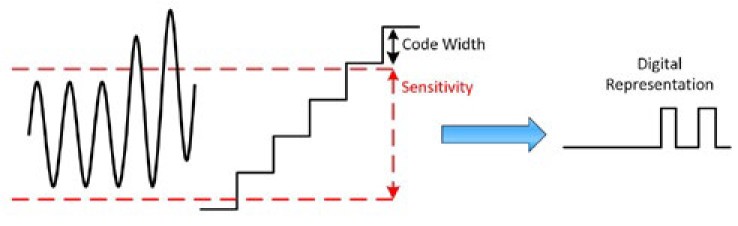
図2:信号が感度レベルを超えると、異なるデジタル値で表される。
計測器の感度の定義方法についても、あいまいな部分があります。場合によっては、上記の例のように、一定量として定義することもできます。この場合、入力信号が感度レベルを超えたとたんに、信号は別のデジタル値で表されます。しかし、信号の変化として定義されることもあります。指定された感度量だけ変化した後で、信号は別の信号として表されます。この場合、絶対電圧ではなく、電圧の変化が重要になります。また、一部の計測器では、感度をゼロ程度と定義しています。
感度という用語の正確な定義は会社ごとに異なるだけでなく、同じ会社でも製品によって多少異なる意味で使用されている場合もあります。計測器の仕様を確認して、感度がどのように定義されているかを確認することが重要です。十分に文書化されていない場合は、その会社に問い合わせてください。
確度
確度とは、計測器が測定対象の信号値を正確に示すことのできる能力と定義されます。この用語は分解能には関連していませんが、確度が計測器の分解能値より大きくなることはありません。
計測器またはデジタイザによって、確度に対する期待値は異なります。たとえば、一般にデジタルマルチメータ (DMM) はオシロスコープよりも高い確度が期待されます。確度の計算方法も計測器によって異なりますが、特定の計測器の確度の計算方法については、必ず計測器の仕様を確認してください。
オシロスコープの確度
オシロスコープは、水平軸システムと垂直軸システムの確度を個別に定義します。水平軸システムは、時間スケールまたはX軸を指します。水平軸システムの確度は、タイムベースの確度です。垂直軸システムは測定された電圧またはY軸です。垂直軸システムの確度は、ゲインとオフセットの確度です。通常、垂直軸システムの確度は水平軸の確度よりも重要です。
垂直軸の確度は通常、入力信号のパーセンテージとフルスケールのパーセンテージで表されます。一部の仕様では、入力信号を垂直ゲインとオフセット確度に分解します。式1は、定義された確度を確認する2つの方法を示しています。
式1:オシロスコープの垂直確度の計算。
たとえば、オシロスコープでは、次の方法で垂直軸確度を定義できます。
10 V入力信号で20 Vレンジを使用すると、確度を計算できます。
DMMと電源の確度
DMMと電源は通常、読み取り値のパーセンテージとして確度を指定します。式2は、DMMまたは電源の確度を表す異なる3つの方法を示しています。
式2:DMMまたは電源の垂直確度の計算。
ppmという用語は、100万分の1を意味します。ほとんどの仕様には、確度を決定するための複数の表があります。確度は、測定タイプ、レンジ、前回のキャリブレーションからの経過時間によって異なります。仕様を確認して、確度の計算方法を確認してください。
たとえば、DMMが10 Vレンジに設定され、キャリブレーション後90日間の間23℃ ± 5℃で動作し、7 V信号を想定します。この条件での確度仕様は、±(読み取り値の20 ppm + レンジの6 ppm) となっています。その後、確度を計算できます。
この場合、読み取り値は実際の入力電圧の200 μV以内である必要があります。
DAQデバイスの確度
DAQカードでは、多くの場合、確度を理想的な伝達関数からの偏差として定義しています。式3は、DAQカードが確度を指定する方法の例を示します。
式3:DAQデバイスの確度の計算。
次に、個々の用語を次のように定義します。
これらの用語の大部分は表で定義され、公称レンジに基づいています。仕様では、ノイズの不確定性の計算も定義します。ノイズの不確定性は、測定におけるノイズの影響による測定の不確定性であり、確度を決定する要因です。
さらに、アナログ入力またはアナログ出力の確度を求めるか、もしくはフィルタが有効か無効かによって、デバイスに複数の確度表が存在する場合があります。
精度
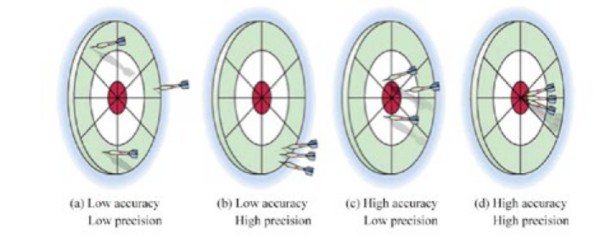
確度と精度は同じ意味でよく使用されますが、わずかな違いがあります。精度は、計測器の安定性の尺度であり、同じ入力信号に対して、繰り返し同じ測定結果にできる能力として定義されます。確度は測定値が真の値にどれだけ近いかということを指すのに対し、精度は各繰り返し測定値がどの程度一致するかを指します。
図3:精度と確度は関連しているが、同じではない。
精度は、計測器のノイズと短期ドリフトの影響を最も受けます。計測器の精度は直接提供されないことはしばしばありますが、伝達比の仕様、ノイズ、温度ドリフトなどの他の仕様から推測する必要があります。ただし、一連の測定値がある場合は、精度を計算できます。
式4:精度の計算。
たとえば、1 Vの定電圧を監視していて、測定ごとに測定値が20 μV変化することに気づいた場合、測定精度は以下のように計算できます。
通常、精度はパーセンテージで表されます。この例では、精度は99.998%です。
精度は主に、デバイスのキャリブレーションなど、相対測定 (同じ値の前回の読み取りに相対) が必要な場合に役立ちます。
ノイズおよびノイズ源
感度を分解能やコード幅と混同しないでください。分解能はコード幅を定義します。これは、計測器が値を表示する離散レベルです。しかし、感度は計測器が値の変化を記録するために必要な電圧の変化を定義します。たとえば、測定範囲が10 Vの計測器は1 mVの分解能で信号を検出できますが、検出可能な最小電圧は15 mVの可能性があります。この場合、計測器の分解能は1 mVですが、感度は15 mVです。
熱ノイズ
理想的な電気回路では、回路自体にはノイズが存在しないため、出力信号中のノイズは元の信号にあったもののみということになります。しかし、実際の電気回路やコンポーネントには、ある程度の固有ノイズが存在します。単純な固定抵抗値の抵抗にもノイズは存在します。
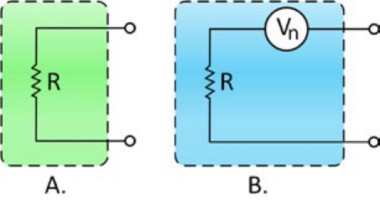
図4:理想的な抵抗はAに反映されるが、実際には抵抗にはBに示すように内部熱ノイズがある。
図4Aは、ノイズのない理想的な抵抗の等価回路を示しています。固有ノイズは、図4Bにノイズなしの理想的な抵抗 (Ri) に直列されたノイズ電圧源 (Vn) として示されています。絶対零度 (0°Kまたは約-273℃) を超える温度では、あらゆる物質内の電子は常にランダムに運動しています。しかし、このランダムな運動特性のため、一定方向に流れる電流を検出することはできません。言い換えれば、ある方向の電子の流れは、相対する反対方向の電子の流れにより瞬く間に相殺されるということです。このため、電子運動は統計的には非相関です。しかし、物質内には一連のランダム電流パルスが絶え間なく生成されており、外界から見た場合、これらのパルスはノイズ信号として認識されます。こういった信号は、ジョンソンノイズ、熱運動ノイズ、または熱ノイズなどと呼ばれています。このノイズは温度と抵抗とともに増加しますが、平方根関数として増加します。つまり、抵抗のノイズを2倍にするには、抵抗を4倍にする必要があることを意味します。
フリッカノイズまたは1/Fノイズ
半導体デバイスには周波数に対して平坦でないノイズが含まれることがあります。このノイズは周波数が低くなるにつれ増加します。これは、1/Fノイズ、ピンクノイズ、過度ノイズ、またはフリッカノイズなどと呼ばれています。このタイプのノイズは、電気以外の物理システムでも発生します。例としては、タンパク質、認知プロセスの反応時間、さらには地震活動などがあります。以下のチャートは、特定の電圧で発生するノイズの周波数に応じた最も可能性の高いノイズの発生源を示します。ノイズの原因を知ることは、ノイズの低減に大きく役立ちます。
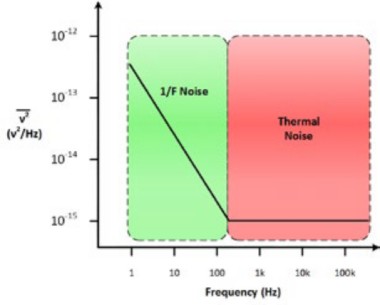
図4:理想的な抵抗はAに反映されるが、実際には抵抗にはBに示すように内部熱ノイズがある。
ノイズ除去の手法
ノイズは、低信号レベルを扱う際には設計者にとって特に大きな問題ですが、複数の一般的な手法により、システムに与えるノイズの影響は軽減できます。ノイズを低減するための戦略をいくつか紹介します。
- ソース抵抗およびアンプ入力抵抗をできる限り小さくします。熱ノイズは抵抗値に比例して増加します。
- 全熱ノイズも回路の帯域幅に比例します。このため、回路の帯域幅を最小にすればノイズも最小になります。しかし、測定の正確性を高めるには信号のフーリエスペクトルを維持しなければならないため、この処理は注意深く実行する必要があります。この解決策として、入力信号に最低限必要な周波数応答に一致するように帯域幅を設定できます。
- 接地、シールド、ケーブル配線、ワイヤを物理的に慎重に配置し、フィルタ処理を適切に使用して、外部ノイズがシステムのパフォーマンスに影響を与えないようにします。
- システムの入力部に低ノイズのアンプを使用します。
- 特定の半導体回路では、機能する最小のDC電源電位を使用します。
まとめ
- 感度とは、測定デバイスが応答を生じる入力信号の最小変化です。
- 確度とは、計測器が測定対象の信号値を正確に示すことのできる能力と定義されます。
- 確度と感度は仕様書に記載されています。会社ごとに異なるだけでなく、同じ会社でも製品によって多少異なる意味で使用されている場合があるため、必ずドキュメントを確認し、必要に応じて会社に問い合わせてください。
- 精度は、計測器の安定性の尺度であり、同じ入力信号に対して、繰り返し同じ測定結果にできる能力として定義されます。
- ノイズは、測定しようとする信号に干渉する不要な信号です。
- ノイズにはさまざまなタイプがあり、ノイズを低減する戦略もさまざまです。
次のステップ
- ノイズを低減するための接地技術について学ぶ
- アンチエイリアスフィルタの仕組みを理解する
- 自動化された特性評価、検証、製造テストに対応するNIのPXI DMM、オシロスコープ、DAQデバイスについて学ぶ
- すべての計測器の基礎コンテンツをダウンロード