Guide to Understanding and Developing an RF Switch Network
Overview
Welcome to the Guide to Understanding and Developing an RF Switch Network, an accumulation of insightful content that arms you with the necessary knowledge to design your RF switch network. This five part document begins by explaining basic RF switch specifications such as insertion loss, VSWR, characteristic impedance, and rise time. It then discuss the importance of switch system design by explaining how choosing the right topology for your application can increase its performance incrementally. The third part of this guide provides you with an overview of the smaller but equally important components that form a part of the switch network, such as cables, and connectors. The fourth part highlights the importance of impedance matching in RF systems using graphs and circuit diagram analysis. Finally, this series of tutorials culminate with a tutorial that discusses the process of picking components and designing an actual RF switch network for optimal performance.
For more information on the RF switch offering from NI visit NI RF Switches main product page.
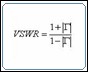 | Chapter 1: Understanding Key RF Switch Specifications This tutorial provides information that helps you decipher the specifications that are often found in the datasheet of an RF switch. It explains in detail concepts such as insertion loss, voltage standing-wave ratio, isolation, rise time, and characteristic impedance. Learn more>> | |
 | Chapter 2: Designing RF Switch Networks This tutorial discusses RF switch specifications from a system perspective. It elaborates on the various use-cases for different RF switch topologies. Furthermore, it uses examples to demonstrate how picking the wrong topology can affect performance significantly. Learn more>> | |
 | Chapter 3: Connection Options for RF Switch Application This tutorial describes in detail the advantages and disadvantages of the various cable and connector options available for RF applications. More... | |
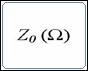 | Chapter 4: Effects of Impedance Matching and Switch Quality on RF Test System Performance This tutorial elaborates further on the definition of voltage standing-wave ratio and the effects of signal reflection that takes place in an RF system due to components with mismatched impedances, using circuit models and graphs. Learn more>> | |
 | Chapter 5: Application Examples This tutorial uses examples of complex RF switch systems to discuss the various considerations when designing the switch network and deploying it using software from a real-world perspective. Learn more >> |