Software Filtering: Windowing - General Analog Concepts
Overview
This tutorial will teach you a specific topic by explaining the theory and giving practical examples. This tutorial covers the theory of using window functions to improve frequency measurements.
For intermediate concepts, please refer to the Grounding Considerations - Intermediate Analog Concepts guide.
Contents
- Definition
- Background - The Fast Fourier Transform (FFT)
- Measuring Over a Finite Interval of Time
- Common Windowing Types
- Windowing in LabVIEW
- Related NI Products
Definition
Windowing is a technique used to shape the time portion of your measurement data, to minimize edge effects that result in spectral leakage in the FFT spectrum. By using Window Functions correctly, the spectral resolution of your frequency-domain result will increase.
Background - The Fast Fourier Transform (FFT)
The FFT, or Fast Fourier Transform, implements a Fourier transform at a discrete set of frequencies and from a time-domain waveform sampled at discrete times over a finite interval of time. Because of the finite interval, the FFT tends not to be very frequency-selective.
The FFT behaves as though it was a bank of narrow-band filters followed by a bank of corresponding detectors that calculate the vector sum of all the signal components that each filter passes. In the case of the power spectrum, the result is scalar instead of vector data, and the detector just indicates the total energy passed by each filter. Again, because of the finite duration of the source data, the filters tend not to be especially selective. There is quite a bit of overlap from bin to bin, as can be seen on figure 1.
As figure 1 also shows, while the main lobe of the filter is reasonably narrow, the sideband response of the filter extends out objectionably. The application of a window function reduces the side lobe responses, at the expense of the width of the main lobe, as can be seen on the figure 5.
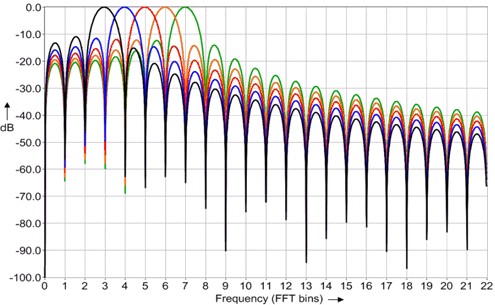
Figure 1. The black curve shows the frequency response of FFT bin 3, blue is bin 4, etc. Not very good rejection of adjacent frequencies.
Measuring Over a Finite Interval of Time
When you use the FFT to measure the frequency content of data, you will have to base the analysis on a finite set of data. The FFT transform assumes that the finite data set is one period of a periodic signal. For the FFT, both the time domain and the frequency domain are circular topologies, so the two endpoints of the time waveform are interpreted as though they were connected together. Therefore, the finiteness of the sampling record may result in a truncated waveform with different spectral characteristics from the original continuous-time signal, and the finiteness can introduce sharp transition changes into the measured data. The sharp transitions are discontinuities. To minimize this effect, we can apply a Window Function to the measured signal in the time domain. This will make the endpoints of the waveform meet and therefore result in a continuous waveform without sharp transitions.
Let's take a look at different cases of finite waveforms.
Integer Number of Periods:
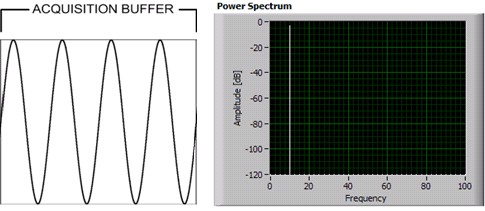
When the signal is periodic and an integer number of periods fill the acquisition time interval, the FFT turns out fine.
Figure 2. Measuring an integer number of periods gives ideal FFT
Non-Integer Number of Periods:
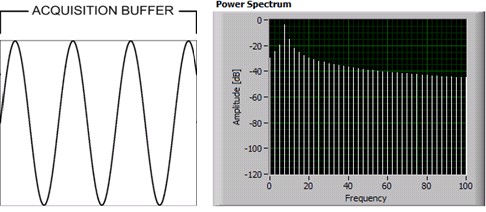
When the number of periods in the acquisition is not an integer, the endpoints are discontinuous. The result is the high side lobes seen in the un-windowed spectrum plot. This phenomena is called Spectral Leakage.
Figure 3. Measuring a non-integer number of periods adds spectral leakage to the FFT
Windowing a Non-Integer of Periods:
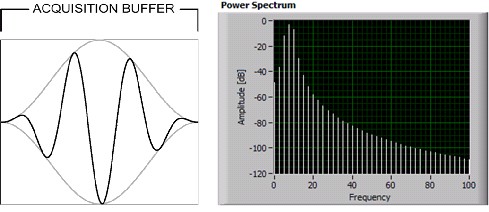
Applying a window function to the acquisition that connects the waveform endpoints in a smoother fashion before computing the FFT, will result in better spectral resolution. This technique is also referred to as 'applying a window' or simply 'windowing'.
Figure 4. Applying a window minimizes the effect of spectral leakage
Common Windowing Types
There are different types of window functions available, each with their own advantage and preferred application. To show the difference between common windows, we will start by looking at an example.
Example of a window:
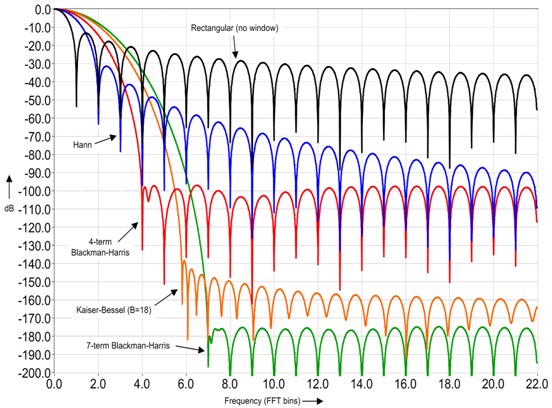
Applying a 4-term Blackman-Harris window before the FFT greatly reduces the side lobes, although the main lobe's -3 dB bandwidth has increased from about 1 bin to about 2 bins (compare figure 5 with figure 1). The extra width is usually worth the trade-off.
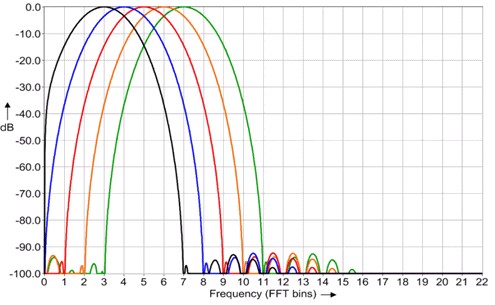
Figure 5. A window (4-term Blackman-Harris) reduces the side lobes in the frequency-domain
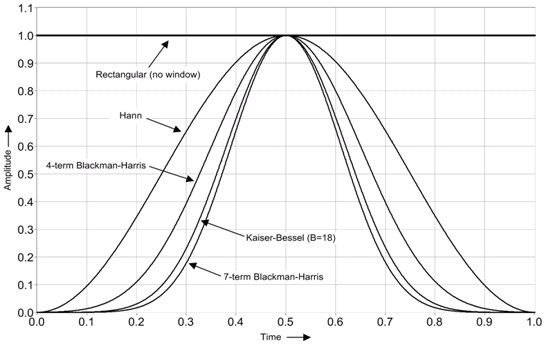
Figure 6 shows the time-domain plot of some common windows. Most windows begin and end at zero and rise to unity in the middle. The narrowest windows in the time domain have the widest main lobes in the frequency domain, and vice-versa.
- Because of the high side lobes, using the FFT with a rectangular window function (or no window function) is normally not recommended.
- The Hann (also called "Hanning") window function is useful for noise measurements where better frequency resolution than some of the other windows is desired but moderate side lobes do not present a problem.
- The 4-term Blackman-Harris window function is a good general purpose window, having side lobe rejection in the high 90s dB and having a moderately wide main lobe.
- The 7-term Blackman-Harris window function has all the dynamic range you should ever need, but it comes with a wide main lobe.
- The Kaiser-Bessel window function has a variable parameter, beta, which trades off side lobes for main lobe. It compares roughly to the Blackman-Harris window functions, but for the same main lobe width, the near side lobes tend to be higher, but the further-out side sidelobes are lower.
As computers get faster and come with more memory, tolerable FFT sizes grow accordingly. Even back in 2000, large FFTs could be computed fast enough that the 7-term Blackman-Harris window provided quite good frequency resolution and, of course, extremely good dynamic range. Future computing horsepower will favor the windows with the highest dynamic range.
Figure 7. The frequency-domain response of the windows from figure 6
Selecting a window function is not a simple task. Each window function has its own characteristics and suitability for different applications. To choose a window function, you must estimate the frequency content of the signal.
- If the signal contains strong interfering frequency components distant from the frequency of interest, choose a smoothing window with a high side lobe roll-off rate.
- If the signal contains strong interfering signals near the frequency of interest, choose a window function with a low maximum side lobe level.
- If the frequency of interest contains two or more signals very near to each other, spectral resolution is important. In this case, it is best to choose a smoothing window with a very narrow main lobe.
- If the amplitude accuracy of a single frequency component is more important than the exact location of the component in a given frequency bin, choose a window with a wide main lobe.
- If the signal spectrum is rather flat or broadband in frequency content, use the uniform window, or no window.
- In general, the Hanning window is satisfactory in 95% of cases. It has good frequency resolution and reduced spectral leakage. If you do not know the nature of the signal but you want to apply a smoothing window, start with the Hanning window.
To get an overview of the what window function to choose with certain signal types and applications, refer to the list in figure 8.
| Type of Signal | Window |
|---|---|
| Transients whose duration is shorter than the length of the window | Rectangular |
| Transients whose duration is longer than the length of the window | Exponential, Hanning |
| General-purpose applications | Hanning |
| Spectral analysis (frequency-response measurements) | Hanning (for random excitation), Rectangular (for pseudorandom excitation) |
| Separation of two tones with frequencies very close to each other but with widely differing amplitudes | Kaiser-Bessel |
| Separation of two tones with frequencies very close to each other but with almost equal amplitudes | Rectangular |
| Accurate single-tone amplitude measurements | Flat top |
| Sine wave or combination of sine waves | Hanning |
| Sine wave and amplitude accuracy is important | Flat top |
| Narrowband random signal (vibration data) | Hanning |
| Broadband random (white noise) | Uniform |
| Closely spaced sine waves | Uniform, Hamming |
| Excitation signals (hammer blow) | Force |
| Response signals | Exponential |
| Unknown content | Hanning |
Windowing in LabVIEW
In LabVIEW Graphical Development software*, windows are available in several frequency-domain functions. For example, the Spectral Measurements Express VI lets you choose between 9 different window types, for your spectral measurements. Since it's an Express VI, you will immediately see an example of the selected window in the time-domain for an easy visual description.
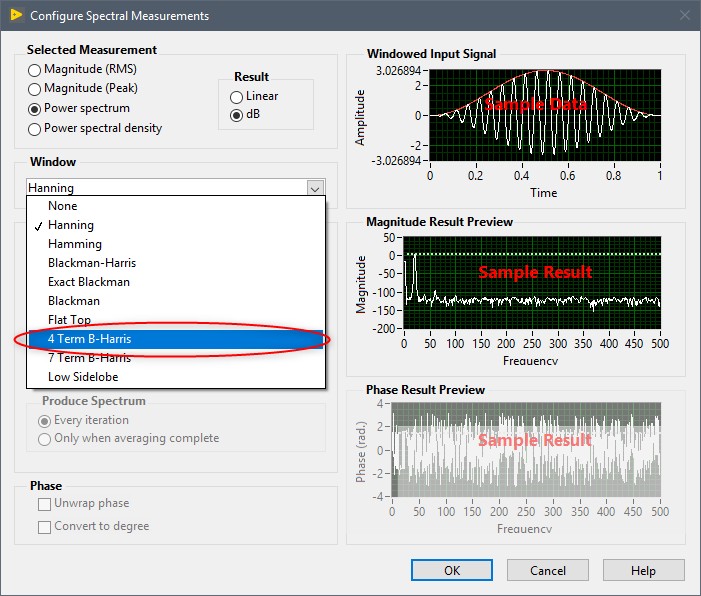
Figure 9. Choosing a window function in the Spectral Measurements Express VI in LabVIEW
Many other VIs includes the option to select your window type. There is even a Windows palette with window function VIs so you can create you own customized analysis application.
Figure 10. The Windows palette in LabVIEW
* Not in the Base Package
Related NI Products
Customers interested in this topic were also interested in the following NI products: