サンプル信号Xの離散積分操作を実行します。


icon

入力/出力

  • c1ddbl.png X —

    Xは時間 0~ n – 1 にサンプリングされた信号です。n は X の要素数です。

  • c1ddbl.png 初期状態 —

    初期状態は積分計算でのXの初期状態を指定します。

    積分方法が 台形の法則 または シンプソンの法則の場合、VIは 初期 条件の最初の要素を使用して積分を計算します。 積分法が シンプソンの3/8則 または ボード則の場合、VIは 初期 条件の最初の2つの要素を使用して積分を計算します。デフォルト値は[0]です。

  • c1ddbl.png 最終状態 —

    最終条件は積分計算でのXの最終条件を指定します。

    積分法が台形公式の場合、VIは最終条件を無視します。 積分方法が シンプソンの法則 または シンプソンの3/8の法則の場合、VIは 最終 条件の最初の要素を使用して積分を計算します。メソッドがボーデの法則の場合、VIは最終条件の最初の2つの要素を使用して積分を計算します。デフォルト値は[0]です。

  • cdbl.png dt —

    dtは、サンプリング間隔で、0よりも大きくなければなりません。デフォルトは1.0です。

    dtが0以下の場合は、Xの積分を空の配列に設定してエラーを返します。

  • ci32.png 積分法 —

    積分法は、数値積分を実行するのに使用する方法を指定します。

    0台形公式
    1シンプソン公式 (デフォルト)
    2シンプソン3/8公式
    3ボーデの法則
  • i1ddbl.png Xの積分 —

    Xの積分は、xの離散積分です。

  • ii32.png エラー —

    エラーは、VIからのエラーまたは警告を返します。エラーは「エラーコードからエラークラスタ」VIに配線して、エラーコードまたは警告をエラークラスタに変換できます。

    • 積分x(t)は、定積分を計算します。任意の値xでの出力配列の値は、入力配列の曲線の下の領域にある0からxの範囲です。

    関数f(t)の積分F(t)は、次のように定義されます。

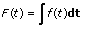
    yはサンプルされた出力シーケンス積分 x(t)を表します。

    積分方法に台形公式を指定すると、VIは y の要素を計算します。

    ここで、i = 0, 1, 2, …, n – 1

    また、nはXのサンプル数、x–1は初期状態の最初の要素です。

    積分方法にシンプソン公式を指定すると、VIは y の要素を計算します。

    ここで、i = 0, 1, 2, …, n – 1

    また、nはXのサンプル数、x–1は初期状態の最初の要素、xnは最終条件の最初の要素です。

    積分方法にシンプソン3/8公式を指定すると、VIは y の要素を計算します。

    ここで、i = 0, 1, 2, …, n – 1

    また、nはXのサンプル数、x–2とx–1は初期状態の最初と2番目の要素、xnは最終条件の最初と2番目の要素です。

    積分方法にボーデの法則を指定すると、VIは y の要素を計算します。

    ここで、i = 0, 1, 2, …, n – 1

    また、nはXのサンプル数、x–2とx–1は初期状態の最初と2番目の要素、xnとxn+1は最終条件の最初と2番目の要素です。

    サンプル数が少ない場合は特に、初期状態と最終条件によって境界での確度が向上して全体のエラーが最小限に抑えられます。確度を向上するために、事前に境界条件を決定します。

    サンプルプログラム

    LabVIEWに含まれている以下のサンプルファイルを参照してください。

    • labview\examples\Mathematics\Probability and Statistics\Probability Density.vi