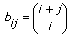Génère une matrice spéciale basée sur le type de la matrice. Le type de données que vous câblez aux entrées Vecteur en entrée 2 et Vecteur en entrée 1 détermine l'instance polymorphe à utiliser.


icon

Entrées/Sorties

  • c1dcdb.png Vecteur en entrée 2 —

    Vecteur en entrée 2 est utilisé en tant qu'entrée pour construire une matrice spéciale dans certaines options.

  • ci32.png type de la matrice —

    type de la matrice spécifie le type de la matrice spéciale utilisée par le VI pour générer la sortie Matrice spéciale.

    Supposons que n représente la taille de la matrice, X représente le Vecteur en entrée 1, nx représente la taille de X, Y représente le Vecteur en entrée 2, ny représente la taille de Y, et B représente la sortie Matrice spéciale.

    0Identité — Génère une matrice identité de type (n, n).
    1Diagonale — Génère une matrice diagonale de type (nx, nx) dont les éléments diagonaux sont les éléments de X.
    2Toeplitz — Génère une matrice de Toeplitz de type (nx, ny), ayant X comme première colonne et Y comme première ligne. Si le 1er élément de X et le 1er élément de Y sont différents, le 1er élément de X est utilisé.
    3

    Vandermonde-Génèreune matrice de Vandermondenx-par-nx dont les colonnes sont des puissances des éléments de X. Les éléments d'une matrice de Vandermonde sont :

    bi,j = xinx – j – 1

    où i,j = 0…nx – 1.

    4

    Compagnon — Génère une matrice compagnon de type (nx-1, nx-1). Si le vecteur X est un vecteur de coefficients polynomiaux, le premier élément de X étant le coefficient de degré le plus élevé et le dernier élément de X étant le terme constant du polynôme, la matrice compagnon correspondante est construite de la manière suivante : la première ligne est

    le reste de B, à partir de la deuxième ligne, est une matrice identité.

    Les valeurs propres d'une matrice compagnon contiennent les racines du polynôme correspondant.

    5Hankel — Génère une matrice de Handel de type (nx, ny), X étant la première colonne et Y la dernière ligne de la matrice. Si le premier élément de Y et le dernier élément de X sont différents, ce VI utilise le dernier élément de X.
    6Hadamard — Génère une matrice de Hadamard de type (n, n) dont les éléments sont 1 et –1. Toutes les colonnes ou lignes sont positionnées de manière orthogonales, les unes par rapport aux autres. taille de la matrice doit être une puissance de 2, une puissance de 2 multipliée par 12 ou une puissance de 2 multipliée par 20. Si n est égal à 1, ce VI renvoie une matrice vide.
    7Wilkinson — Génère une matrice de Wilkinson de type (n, n) dont les valeurs propres sont mal conditionnées.
    8

    Hilbert — Génère une matrice de Hilbert symétrique de type (n, n) qui a des éléments en fonction de la formule suivante :

    où i,j = 0,1,…n – 1

    9Hibert inverse — Génère l'inverse d'une matrice de Hilbert de type (n, n).
    10Rosser — Génère une matrice de Rosser de type (8, 8), dans laquelle les valeurs propres sont mal conditionnées.
    11

    Pascal — Génère une matrice de Pascal symétrique de type (n, n) qui a des éléments en fonction de la formule suivante :

    où i,j = 0,1,…n – 1

  • ci32.png taille de la matrice —

    taille de la matrice détermine la dimension de la Matrice spéciale de sortie.

  • c1dcdb.png Vecteur en entrée 1 —

    Vecteur en entrée 1 est utilisé en tant qu'entrée pour construire une matrice spéciale dans certaines options.

  • i2dcdb.png Matrice spéciale —

    Matrice spéciale est la matrice générée.

  • ii32.png erreur —

    erreur renvoie toute erreur ou mise en garde générée par le VI. Vous pouvez câbler erreur au VI Convertir un code d'erreur en cluster d'erreur pour convertir le code d'erreur ou la mise en garde en cluster d'erreur.

    • Exemples

    Reportez-vous aux exemples de fichiers inclus avec LabVIEW suivants.

    • labview\examples\Mathematics\Linear Algebra\Matrix to a Power.vi